Ta có: \(AB//CD\left(Gt\right)\)
Áp dụng định lí ta - let trong hình thang \(ABCD\)ta có:
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA.OD=OB.OC\left(đpcm\right)\)
Các câu hỏi tương tự
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O
Chứng minh rằng: OA.OD = OB.OC
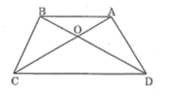
Cho hình thang ABCD (AB // CD), có 2 đường chéo AC và BD cắt tại O. Chứng minh rằng OA.OD = OB.OC
cho hình thang ABCD(AB//CD) có 2 đường chéo AC, BD cắt nhau tại O. Chứng minh: OA.OD=OB.OC
Help me !!!
Cho hình thang ABCD có hai đáy là AB và CD, các đường chéo cắt nhau tại O. Chứng minh O A . O D = O B . O C .
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD. a) Chứng minh rằng OA.OD OB.OC b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K. Chứng minh rằng
O
H
O
K
A
B
C
D
Đọc tiếp
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng OA.OD = OB.OC
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
Chứng minh rằng O H O K = A B C D
hình thang abcd (ab//cd).Hai đường chéo ac và bd cắt nhau tại 0.a,chứng minh rằng: tam giác oad và tam giác obc có diện tích bằng nhau. b,ad cắt bc tại k.chứng minh rằng đường thẳng ok đi qua trung điểm của ab và cd
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: O M O N = A B C D
Cho hình thang ABCD(AB//BC) và O là giao điểm của hai đường chéo AC và BD
a) Chứng minh OA.OD=OB.OC
b) Đường thẳng qua O vuông góc với AB cắt AB và CD lần lượt tại H và K . Chứng minh OH.CD=OK.AB
1.Cho hình thang ABCD (AB//CD) và O là giao điểm của hai đường chéo AC và BD
a) Chứng minh OA.OD = OB.OC
b) Đường thẳng qua O vuông góc với AB cắt AB và CD lần lượt tại H và K . Chứng minh OH.CD = OK.AB