Question

Hình thang ABCD có đáy lớn CD=20m, đáy nhỏ AB= 15m, M là 1 điểm trên AB cách B 5m. Nối M với C. Tính diện tích AMCD biết diện tích tam giác BMC = 280 m2

 

Answer 1

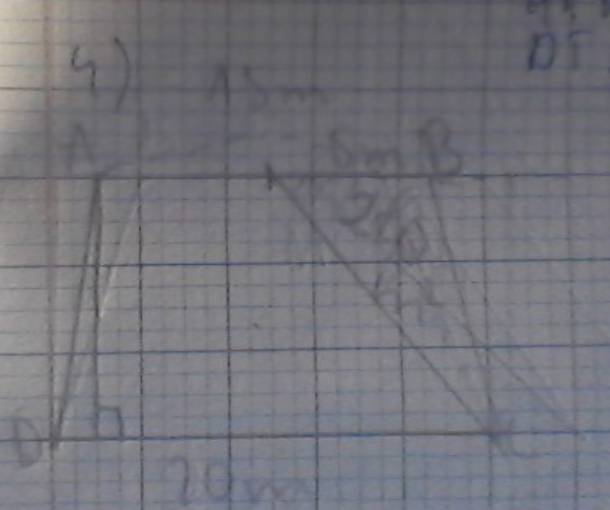
Kẻ CK⊥AB tại K

=>CK là đường cao của hình thang ABCD

Xét hình thang ABCD có CK là đường cao

nên \(S_{ABCD}=\frac12\times CK\times\left(AB+CD\right)=\frac12\times CK\times\left(20+15\right)=17,5\times CK\)

Diện tích tam giác MBC là:

\(S_{MBC}=\frac12\times KC\times MB=\frac12\times5\times KC=2,5\times KC\)

=>\(2,5\times KC=280\)

=>KC=280:2,5=112(cm)

=>\(S_{ABCD}=17,5\times112=1960\left(\operatorname{cm}^2\right)\)

Ta có: \(S_{MBC}+S_{AMCD}=S_{ABCD}\)

=>\(S_{AMCD}=1960-280=1680\left(\operatorname{cm}^2\right)\)