Các câu hỏi tương tự
Xét trong mặt phẳng, hình nào không có trục đối xứng trong các hình dưới đây?
A. Hình chữ nhật
B. Hình tam giác đều
C. Hình thang cân
D. Hình bình hành
Xét trong mặt phẳng, hình nào không có trục đối xứng trong các hình dưới đây?
A. Hình chữ nhật
B. Hình tam giác đều
C. Hình thang cân
D. Hình bình hành
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A,B,C,D và hai đường parabol có các đỉnh lần lượt là E,F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M,N,P,Q. Biết AB8m,CD6m,
M
N
P
Q
3
3
m
, EF2m. Chi phí để trồng hoa trên vường là
300
.
000...
Đọc tiếp
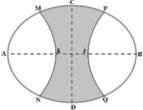
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A,B,C,D và hai đường parabol có các đỉnh lần lượt là E,F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M,N,P,Q. Biết AB=8m,CD=6m, M N = P Q = 3 3 m , EF=2m. Chi phí để trồng hoa trên vường là 300 . 000 đồng/ m 2 . Hỏi số tiền trồng hoa của vườn gần nhất với kết quả nào dưới đây?
A. 4.477.800 đồng
B. 4.470.000 đồng
C. 4.908.815 đồng
D. 4.809.142 đồng
Cho hình thang cân ABCD có các cạnh AB2a, CD4a và cạnh bên ADBC3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó. A.
V
4
3
π
a
3
B.
V
4
+
10
2
3...
Đọc tiếp
Cho hình thang cân ABCD có các cạnh AB=2a, CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A. V = 4 3 π a 3
B. V = 4 + 10 2 3 π a 3
C. V = 10 2 3 π a 3
D. V = 14 2 3 π a 3
Cho hình thang cân ABCD có các cạnh đáy AB 2a, CD 4a và cạnh bên AD BC 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó. A.
V
4
3
πa
3
B.
V
4
+
10
2
3
πa
3
C....
Đọc tiếp
Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
A. V = 4 3 πa 3
B. V = 4 + 10 2 3 πa 3
C. V = 10 2 3 πa 3
D. V = 14 2 3 πa 3
Trong sân vườn của một trường học, người ta dự định làm một vườn hoa hình elip và được chia ra làm 4 phần bởi 2 đường parabol có chung đỉnh, đối xứng nhau qua trục của elip (hình vẽ). Biết độ dài trục lớn trục nhỏ của elip lần lượt là 8m và 4m,
F
1
,
F
2
là hai tiêu điểm. Phần A, B để trồng hoa, phần C, D sẽ trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đồng và 150.000 đồng. tổng số t...
Đọc tiếp
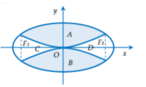
Trong sân vườn của một trường học, người ta dự định làm một vườn hoa hình elip và được chia ra làm 4 phần bởi 2 đường parabol có chung đỉnh, đối xứng nhau qua trục của elip (hình vẽ). Biết độ dài trục lớn trục nhỏ của elip lần lượt là 8m và 4m, F 1 , F 2 là hai tiêu điểm. Phần A, B để trồng hoa, phần C, D sẽ trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đồng và 150.000 đồng. tổng số tiền để hoàn thành vường hoa (làm tròn đến hàng nghìn) gần nhất với số tiền nào dưới đây ?
A. 4.656.000 đồng
B. 5.455.000 đồng
C. 5.676.000 đồng
D. 4.766.000 đồng
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
. Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hình chóp là A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
.
Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hìn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho một hình thang cân ABCD có cạnh đáy
A
B
2
a
,
C
D
4
a
, cạnh bên
A
D
B
C
3
a
. Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó. A.
4
2
π...
Đọc tiếp
Cho một hình thang cân ABCD có cạnh đáy A B = 2 a , C D = 4 a , cạnh bên A D = B C = 3 a . Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
A. 4 2 π a 3 3
B. 56 2 π a 3 3
C. 16 2 π a 3 3
D. 14 2 π a 3 3



