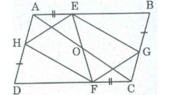
+) Ta có: AH + HD = AD
CG + GB = CB
Mà AD = CB ( vì ABCD là hình bình hành).
DH = GB ( giả thiết)
Suy ra: AH = CG.
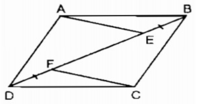
Xét ∆ AEH và ∆ CFG:
AE = CF (gt)
∠ A = ∠ C (tính chất hình bình hành)
AH = CG ( chứng minh trên).
Do đó: ∆ AEH = ∆ CFG (c.g.c)
⇒ EH = FG
Xét ∆ BEG và ∆ DFH, ta có:
BG = DH (gt)
∠ B = ∠ D (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )
Do đó: ∆ BEG = ∆ DFH (c.g.c) ⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)