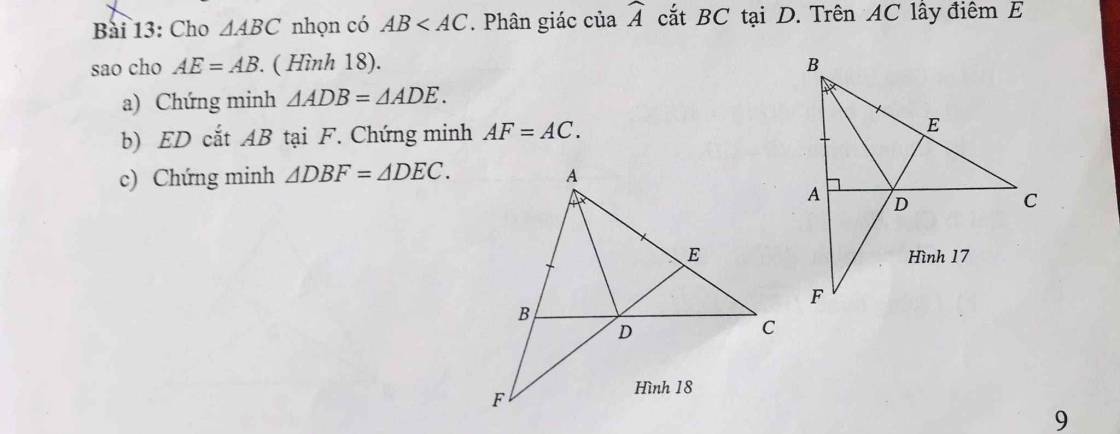
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: ΔABD=ΔAED
=>AB=AE và \(\widehat{ABD}=\widehat{AED}\)
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)
AE=AB
\(\widehat{FAE}\) chung
Do đó: ΔAEF=ΔABC
=>AF=AC
c: AB+FB=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=CE
\(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó:ΔDBF=ΔDEC
Đúng 1
Bình luận (0)
