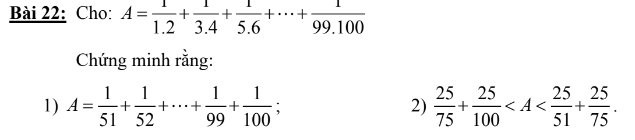Lời giải:
1.
$A=\frac{2-1}{1.2}+\frac{4-3}{3.4}+\frac{6-5}{5.6}+....+\frac{100-99}{99.100}$
$=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+....+\frac{1}{99}-\frac{1}{100}$
$=(1+\frac{1}{3}+\frac{1}{5}+....+\frac{1}{99})-(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+....+\frac{1}{100})$
$=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+....+\frac{1}{99}+\frac{1}{100})-2(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+....+\frac{1}{100})$
$=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+....+\frac{1}{99}+\frac{1}{100})-(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{50})$
$=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{100}$
2.
$A=(\frac{1}{51}+\frac{1}{52}+....+\frac{1}{75})+(\frac{1}{76}+\frac{1}{77}+...+\frac{1}{100})$
$< (\frac{1}{51}+\frac{1}{51}+...+\frac{1}{51})+(\frac{1}{75}+\frac{1}{75}+....+\frac{1}{75})$
$=\frac{25}{51}+\frac{25}{75}$
Lại có:
$A=(\frac{1}{51}+\frac{1}{52}+....+\frac{1}{75})+(\frac{1}{76}+\frac{1}{77}+...+\frac{1}{100})$
$>(\frac{1}{75}+\frac{1}{75}+...+\frac{1}{75})+(\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100})$
$=\frac{25}{75}+\frac{25}{100}$
Vậy ta có đpcm.