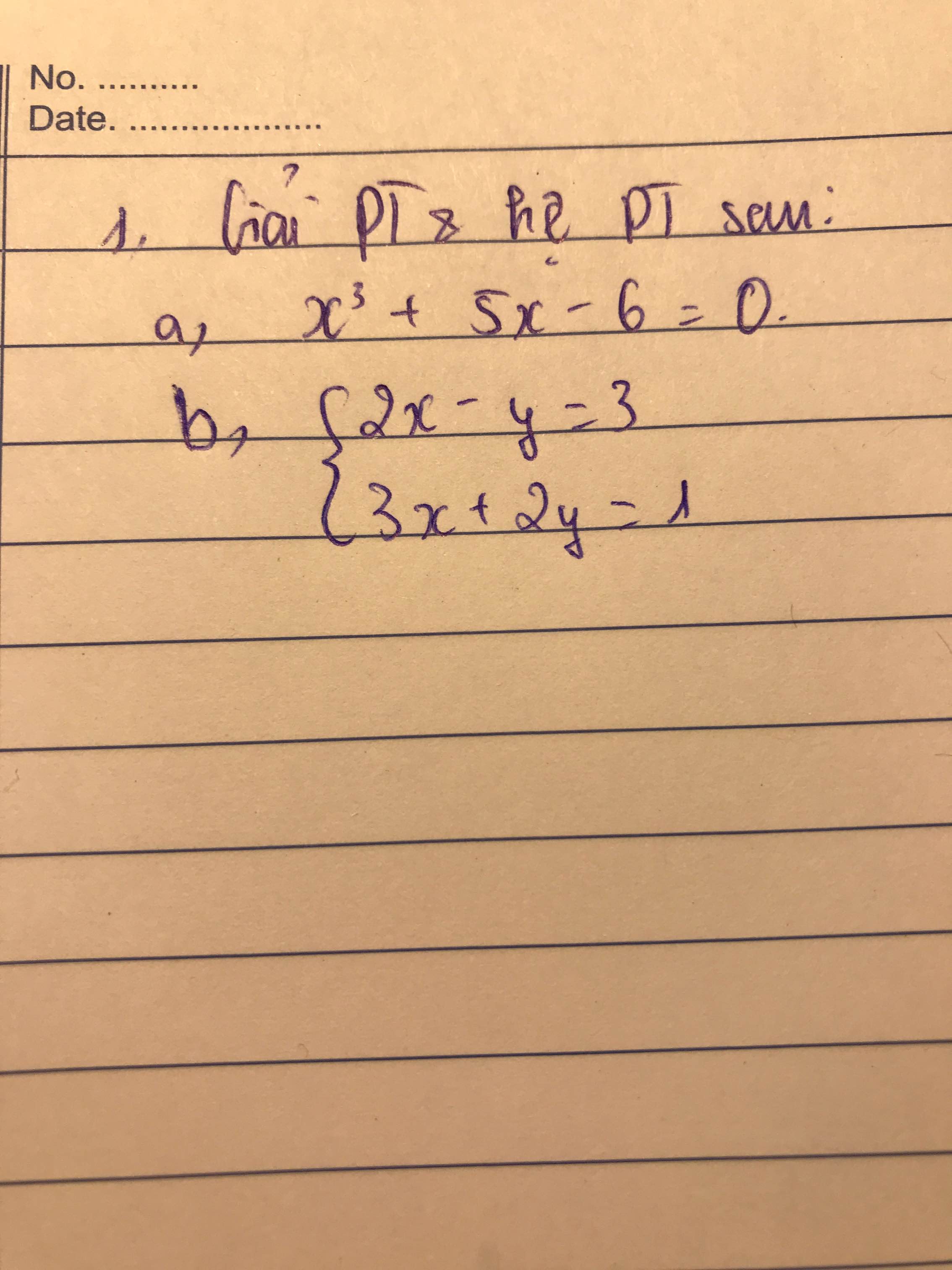\(a,x^3+5x-6=0\\ \Leftrightarrow\left(x^3-x^2\right)+\left(x^2-x\right)+\left(6x-6\right)=0\\ \Leftrightarrow x^2\left(x-1\right)+x\left(x-1\right)+6\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{23}{4}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x+\dfrac{1}{2}\right)^2=-\dfrac{23}{4}\left(vô.lí\right)\end{matrix}\right.\)
\(b,\left\{{}\begin{matrix}2x-y=3\\3x+2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x-2y=6\\3x+2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7x=7\\2x-y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\2.1-y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\2-y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
a) \(x^3+5x-6=0\Leftrightarrow x^3-x+6x-6=0\)
\(\Leftrightarrow\left(x^2-1\right)x+6\left(x-1\right)=0\\\Leftrightarrow\left(x-1\right)\left(x+1\right)x+\left(x-1\right)6=0\\\Leftrightarrow\left(x-1\right)\left(x^2+x+6\right)=0 \)
\(\Leftrightarrow x-1=0 \)(vì ta luôn đúng với \(x^2\ge0\Leftrightarrow x^2+x+6\ge x+6\))
\(\Leftrightarrow x=1\)
➤ \(x=1\)
b) \(\left\{{}\begin{matrix}2x-y=3\\3x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-3y=9\\6x+4y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=3\Leftrightarrow2x=y+3\\7y=2-9=-7\Leftrightarrow y=\dfrac{-7}{7}=-1\end{matrix}\right.\)
Do hệ phương trình trên có \(y=-1\), nên: \(2x=y+3=3-1=2\)
\(\Leftrightarrow x=1\)
➤\(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)