Bài 1:
\(a,4\dfrac{1}{3}-2\dfrac{3}{4}\)
\(=\dfrac{13}{3}-\dfrac{11}{4}\)
\(=\dfrac{52}{12}-\dfrac{33}{12}\)
\(=\dfrac{19}{12}\)
\(\)\(b,-3,72-\left(5,7-9,42\right)\)
\(=\dfrac{-93}{25}-\left(\dfrac{57}{10}-\dfrac{471}{50}\right)\)
\(=\dfrac{-93}{25}-\dfrac{57}{10}+\dfrac{471}{50}\)
\(=\dfrac{-186}{50}-\dfrac{285}{50}+\dfrac{471}{50}\)
\(=\dfrac{\left(-186\right)-285+471}{50}\)
\(=0\)
\(c,2\dfrac{3}{4}-\dfrac{1}{8}+\left(-1\dfrac{1}{2}\right)\)
\(=\dfrac{11}{4}-\dfrac{1}{8}-\dfrac{3}{2}\)
\(=\dfrac{22}{8}-\dfrac{1}{8}-\dfrac{12}{8}\)
\(=\dfrac{9}{8}\)
\(d,0,75-\dfrac{5}{6}+1\dfrac{1}{2}\)
\(=\dfrac{3}{4}-\dfrac{5}{6}+\dfrac{3}{2}\)
\(=\dfrac{9}{12}-\dfrac{10}{12}+\dfrac{18}{12}\)
\(=\dfrac{17}{12}\)
\(e,\dfrac{3}{7}+\dfrac{4}{15}+\left(\dfrac{-8}{21}\right)+\left(-0,4\right)\)
\(=\dfrac{3}{7}+\dfrac{4}{15}-\dfrac{8}{21}-\dfrac{2}{5}\)
\(=\left(\dfrac{3}{7}-\dfrac{8}{21}\right)+\left(\dfrac{4}{15}-\dfrac{2}{5}\right)\)
\(=\left(\dfrac{9}{21}-\dfrac{8}{21}\right)+\left(\dfrac{4}{15}-\dfrac{6}{15}\right)\)
\(=\dfrac{1}{21}+\dfrac{-2}{15}\)
\(=\dfrac{5}{105}+\dfrac{-14}{105}\)
\(=\dfrac{-9}{105}=\dfrac{-3}{35}\)
\(f,0,625+\left(\dfrac{-2}{7}\right)+\dfrac{3}{8}+\left(\dfrac{-5}{7}\right)+1\dfrac{2}{3}\)
\(=\dfrac{5}{8}-\dfrac{2}{7}+\dfrac{3}{8}-\dfrac{5}{7}+\dfrac{5}{3}\)
\(=\left(\dfrac{5}{8}+\dfrac{3}{8}\right)-\left(\dfrac{2}{7}+\dfrac{5}{7}\right)+\dfrac{5}{3}\)
\(=1-1+\dfrac{5}{3}\)
\(=\dfrac{5}{3}\)
Bài 3:
\(a,x-\dfrac{1}{4}=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}+\dfrac{1}{4}\)
\(x=\dfrac{4}{12}+\dfrac{3}{12}\)
\(x=\dfrac{7}{12}\)
Vậy \(x=\dfrac{7}{12}\)
\(b,x-\dfrac{2}{5}=-1\dfrac{1}{2}\)
\(x-\dfrac{2}{5}=\dfrac{-3}{2}\)
\(x=\dfrac{-3}{2}+\dfrac{2}{5}\)
\(x=\dfrac{-15}{10}+\dfrac{4}{10}\)
\(x=\dfrac{-11}{10}\)
Vậy \(x=\dfrac{-11}{10}\)
\(c,-x+\dfrac{3}{10}=-\dfrac{2}{5}\)
\(-x=\dfrac{-2}{5}-\dfrac{3}{10}\)
\(-x=\dfrac{-4}{10}-\dfrac{3}{10}\)
\(-x=\dfrac{-7}{10}\)
\(x=\dfrac{7}{10}\)
Vậy \(x=\dfrac{7}{10}\)
\(d,x+\dfrac{2}{3}=\dfrac{3}{5}-\left(-\dfrac{1}{6}\right)\)
\(x+\dfrac{2}{3}=\dfrac{3}{5}+\dfrac{1}{6}\)
\(x+\dfrac{2}{3}=\dfrac{18}{30}+\dfrac{5}{30}\)
\(x+\dfrac{2}{3}=\dfrac{23}{30}\)
\(x=\dfrac{23}{30}-\dfrac{2}{3}\)
\(x=\dfrac{23}{30}-\dfrac{20}{30}\)
\(x=\dfrac{3}{30}\)
\(x=\dfrac{1}{10}\)
Vậy \(x=\dfrac{1}{10}\)
\(e,\dfrac{7}{4}-\left(x+\dfrac{5}{3}\right)=\dfrac{-12}{5}\)
\(x+\dfrac{5}{3}=\dfrac{7}{4}-\dfrac{-12}{5}\)
\(x+\dfrac{5}{3}=\dfrac{7}{4}+\dfrac{12}{5}\)
\(x+\dfrac{5}{3}=\dfrac{35}{20}+\dfrac{48}{20}\)
\(x+\dfrac{5}{3}=\dfrac{83}{20}\)
\(x=\dfrac{83}{20}-\dfrac{5}{3}\)
\(x=\dfrac{249}{60}-\dfrac{100}{60}\)
\(x=\dfrac{149}{60}\)
\(f,x-\left[\dfrac{17}{2}-\left(\dfrac{-3}{7}+\dfrac{5}{3}\right)\right]=\dfrac{-1}{3}\)
\(x-\left[\dfrac{17}{2}-\left(\dfrac{-9}{21}+\dfrac{35}{21}\right)\right]=\dfrac{-1}{3}\)
\(x-\left[\dfrac{17}{2}-\dfrac{26}{21}\right]=\dfrac{-1}{3}\)
\(x-\left[\dfrac{357}{42}-\dfrac{52}{42}\right]=\dfrac{-1}{3}\)
\(x-\dfrac{305}{42}=\dfrac{-1}{3}\)
\(x=\dfrac{-1}{3}+\dfrac{305}{42}\)
\(x=\dfrac{-14}{42}+\dfrac{305}{42}\)
\(x=\dfrac{291}{42}\)
\(x=\dfrac{97}{14}\)


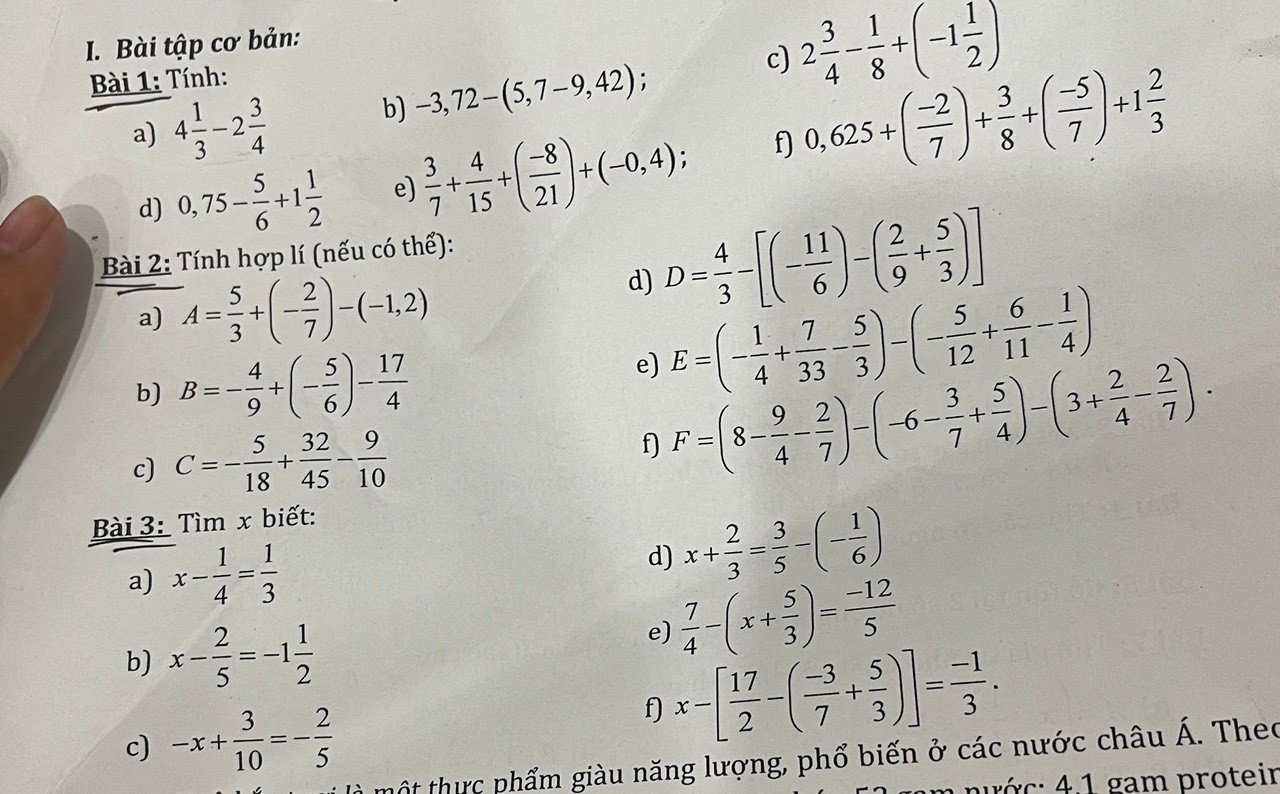











 help tui có làm đk
help tui có làm đk
 HELP ME TUI ĐANG CẦN GẤP !!!
HELP ME TUI ĐANG CẦN GẤP !!!
