Help me PLS
a: \(D=\frac{1}{1\cdot1981}+\frac{1}{2\cdot1982}+\cdots+\frac{1}{25\cdot2005}\)
\(=\frac{1}{1980}\left(\frac{1980}{1\cdot1981}+\frac{1980}{2\cdot1982}+\cdots+\frac{1980}{25\cdot2005}\right)\)
\(=\frac{1}{1980}\left(1-\frac{1}{1981}+\frac12-\frac{1}{1982}+\cdots+\frac{1}{25}-\frac{1}{2005}\right)\)
\(=\frac{1}{1980}\left(1+\frac12+\cdots+\frac{1}{25}-\frac{1}{1981}-\frac{1}{1982}-\cdots-\frac{1}{2005}\right)\)
\(E=\frac{1}{1\cdot26}+\frac{1}{2\cdot27}+\cdots+\frac{1}{1980\cdot2005}\)
\(=\frac{1}{25}\left(\frac{25}{1\cdot26}+\frac{25}{2\cdot27}+\cdots+\frac{25}{1980\cdot2005}\right)\)
\(=\frac{1}{25}\left(1-\frac{1}{26}+\frac12-\frac{1}{27}+\cdots+\frac{1}{1980}-\frac{1}{2005}\right)\)
\(=\frac{1}{25}\left(1+\frac12+\cdots+\frac{1}{25}-\frac{1}{1981}-\frac{1}{1982}-\cdots-\frac{1}{2005}\right)\)
DO đó: \(\frac{D}{E}=\frac{1}{1980}:\frac{1}{25}=\frac{25}{1980}=\frac{5}{396}\)
b: \(A=133\left(\frac{1}{1\cdot1996}+\frac{1}{2\cdot1997}+\cdots+\frac{1}{17\cdot2012}\right)\)
\(=\frac{133}{1995}\left(\frac{1995}{1\cdot1996}+\frac{1995}{2\cdot1997}+\cdots+\frac{1995}{17\cdot2012}\right)\)
\(=\frac{1}{15}\left(1-\frac{1}{1996}+\frac12-\frac{1}{1997}+\cdots+\frac{1}{17}-\frac{1}{2012}\right)\)
\(=\frac{1}{15}\left(1+\frac12+\cdots+\frac{1}{17}-\frac{1}{1996}-\frac{1}{1997}-\cdots-\frac{1}{2012}\right)\)
\(B=\frac{17}{15}\left(\frac{1}{1\cdot18}+\frac{1}{2\cdot19}+\cdots+\frac{1}{1995\cdot2012}\right)\)
\(=\frac{1}{15}\left(\frac{17}{1\cdot18}+\frac{17}{2\cdot19}+\cdots+\frac{17}{1995\cdot2012}\right)\)
\(=\frac{1}{15}\left(1-\frac{1}{18}+\frac12-\frac{1}{19}+\cdots+\frac{1}{1995}-\frac{1}{2012}\right)\)
\(=\frac{1}{15}\left(1+\frac12+\cdots+\frac{1}{17}-\frac{1}{1996}-\frac{1}{1997}-\cdots-\frac{1}{2012}\right)\)
Do đó: A=B
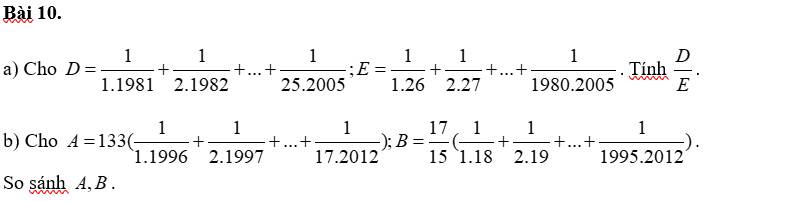help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với