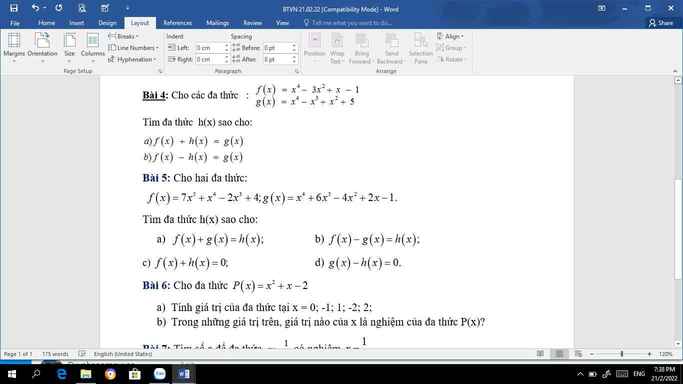
a) Xét \(\Delta BAD:AB=BD\left(gt\right).\Rightarrow\Delta BAD\) cân tại B.
Mà \(\widehat{B}=60^o\left(gt\right).\)
\(\Rightarrow\Delta BAD\) đều.
b) Xét \(\Delta ABI\) và \(\Delta DBI:\)
BI chung.
AB = DB (gt).
\(\widehat{ABI}=\widehat{DBI}\) (BI là phân giác).
\(\Rightarrow\) \(\Delta ABI=\) \(\Delta DBI\left(c-g-c\right).\)
c) \(\Delta ABD\) đều (cmt).
\(\Rightarrow AB=BD=6\left(cm\right).\)
BI là phân giác góc B (gt).
\(\Rightarrow\widehat{IBC}=60^o.\)
Xét \(\Delta ABC\) vuông tại A: \(\widehat{B}=60^o\left(gt\right).\Rightarrow\widehat{C}=30^o.\)
Xét \(\Delta IBC:\widehat{IBC}=I\widehat{CB}\left(=60^o\right).\)
\(\Rightarrow\Delta IBC\) cân tại I.
Mà ID là đường cao \(\left(ID\perp BC\right).\)
\(\Rightarrow\) ID là trung tuyến.
\(\Rightarrow\) D là trung điểm BC.
\(\Rightarrow BC=2BD=2.6=12\left(cm\right).\)