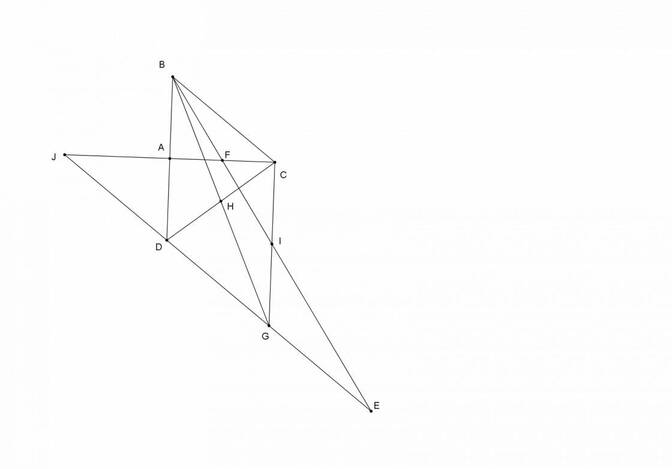
gọi $J$ là giao điểm của $DE,AC$, ta có $BCDJ $là hình thoi nên $BC\parallel JD$, $JA=AC=2CF\Rightarrow 3CF=JF$, theo Thales ta có \(\dfrac{BC}{EJ}=\dfrac{CF}{JF}=\dfrac{1}{3}\Rightarrow JE=3BC\), mà $JD=BC$ nên suy ra $DE=2BC$, hay $EG=DG=BC$, dẫn đến $BCEG,BCGD$ là hình bình hành, suy ra $H$ là trung điểm $CD,I$ là trung điểm $CG$, theo tính chất đường trung bình ta có \(IH=\dfrac{1}{2}DG=\dfrac{1}{4}DE\)










