s: \(\dfrac{-21}{46}\cdot\left(-13\right)+\dfrac{3^2}{-9}-\dfrac{-1}{2}\cdot\left(-10\right)\)
\(=\dfrac{21}{46}\cdot13-1-\dfrac{1}{2}\cdot10\)
\(=\dfrac{273}{46}-1-5=\dfrac{273}{46}-5=\dfrac{43}{46}\)
t: \(T=\left(-\dfrac{1}{7}\right)+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2024}\)
=>\(\left(-\dfrac{1}{7}\right)\cdot T=\left(-\dfrac{1}{7}\right)^2+\left(-\dfrac{1}{7}\right)^3+...+\left(-\dfrac{1}{7}\right)^{2025}\)
=>\(\left(-\dfrac{1}{7}\right)\cdot T-T=\left(-\dfrac{1}{7}\right)^2+\left(-\dfrac{1}{7}\right)^3+...+\left(-\dfrac{1}{7}\right)^{2025}-\left(-\dfrac{1}{7}\right)-\left(-\dfrac{1}{7}\right)^2-...-\left(-\dfrac{1}{7}\right)^{2024}\)
=>\(-\dfrac{8}{7}T=\left(-\dfrac{1}{7}\right)^{2025}+\dfrac{1}{7}\)
=>\(-\dfrac{8}{7}\cdot T=-\dfrac{1}{7^{2025}}+\dfrac{1}{7}\)
=>\(-\dfrac{8}{7}\cdot T=\dfrac{-1+7^{2024}}{7^{2025}}\)
=>\(T\cdot\dfrac{8}{7}=\dfrac{-7^{2024}+1}{7^{2025}}\)
=>\(T=\dfrac{-7^{2024}+1}{7^{2025}}:\dfrac{8}{7}=\dfrac{-7^{2024}+1}{7^{2024}}\cdot8\)
u: \(U=\dfrac{1}{5}-\dfrac{1}{5^2}+\dfrac{1}{5^3}-...-\dfrac{1}{5^{2024}}\)
=>\(5\cdot U=1-\dfrac{1}{5}+\dfrac{1}{5^2}-...-\dfrac{1}{5^{2023}}\)
=>\(5U+U=1-\dfrac{1}{5}+\dfrac{1}{5^2}-...-\dfrac{1}{5^{2023}}+\dfrac{1}{5}-\dfrac{1}{5^2}+...-\dfrac{1}{5^{2024}}\)
=>\(6U=1-\dfrac{1}{5^{2024}}=\dfrac{5^{2024}-1}{5^{2024}}\)
=>\(U=\dfrac{5^{2024}-1}{5^{2024}\cdot6}\)

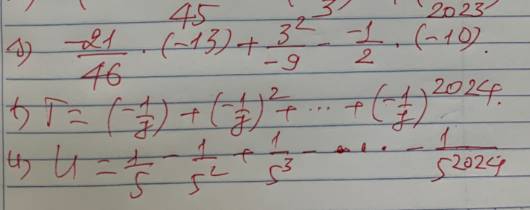











 help bài 7 vs huhu
help bài 7 vs huhu

 giúp em phần C bt tự luyện vs ạ
giúp em phần C bt tự luyện vs ạ