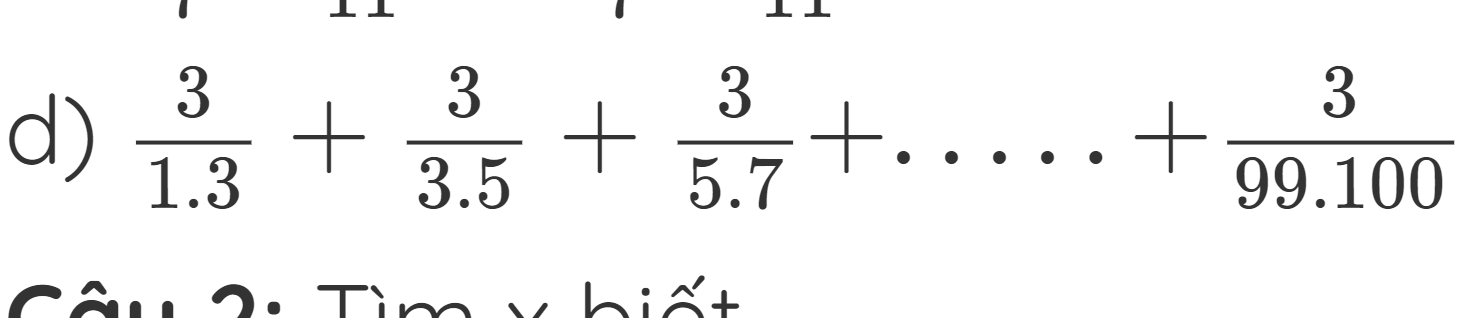Question

hãy giải và nêu cách làm

Answer 1

 

Answer 2

d) \(\dfrac{3}{1\cdot3}+\dfrac{3}{3\cdot5}+\dfrac{3}{5\cdot7}+...+\dfrac{3}{99\cdot100}\)

\(=\)    \(\dfrac{3\cdot1}{1\cdot3}+\dfrac{3\cdot1}{3\cdot5}+\dfrac{3\cdot1}{5\cdot7}+...+\dfrac{3\cdot1}{99\cdot100}\)

\(=3\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=3\cdot\dfrac{1}{2}\cdot\left(1-\dfrac{1}{100}\right)\)

\(=\dfrac{3}{2}\cdot\dfrac{99}{100}\)

\(=\dfrac{297}{200}\)