(Lưu ý: Các phần giải thích các bạn có thể không trình bày vào bài làm)
2 x 2 + 5 x + 2 = 0 ⇔ 2 x 2 + 5 x = − 2
(Chuyển 2 sang vế phải)
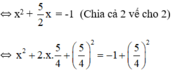
(Tách 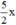 thành
thành 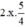 và thêm bớt
và thêm bớt 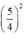 để vế trái thành bình phương).
để vế trái thành bình phương).
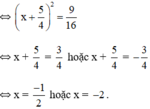
Vậy phương trình có hai nghiệm 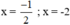
(Lưu ý: Các phần giải thích các bạn có thể không trình bày vào bài làm)
2 x 2 + 5 x + 2 = 0 ⇔ 2 x 2 + 5 x = − 2
(Chuyển 2 sang vế phải)
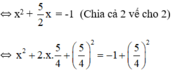
(Tách 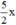 thành
thành 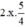 và thêm bớt
và thêm bớt 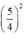 để vế trái thành bình phương).
để vế trái thành bình phương).
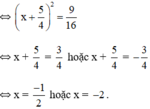
Vậy phương trình có hai nghiệm 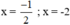
Hãy giải phương trình : 2x2 + 5x + 2 = 0 theo các bước như ví dụ 3 trong bài học.
câu tiếp theo nà:
Hãy giải phương trình:
2x^2+5x+2=0
Theo các bước như ví dụ 3 trong bài học.
mong các bạn giúp đỡ =))
bài 1: giải các phương trình sau :
a) x^3-5x=0 b) căn bậc 2 của x-1=3
bài 2 :
cho hệ phương trình : {2x+my;3x-y=0 (I)
a) giải hệ phương trình khi m=0
b) tìm giá trị của m để hệ (I) có nghiệm (x;y) thỏa mãn hệ thức :
x-y+m+1/m-2=-4
bài 3:giải các phương trình sau
a)5x-2/3=5x-3/2 b) 10x+3/12=1+6x+8/9 c) 2(x+3/5)=5-(13/5+x) d) 7/8x-5(x-9)=20x+1,5/6
Bài 1: Cho phương trình : x ^ 2 - 8x - 33 = 0 a/ Chứng tỏ Pt luôn có nghiệm.Không giải phương trình,hãy tính tổng,tích các nghiệm b/Tính giá trị A=3(x 1 +x 2 )^ 2 -2x 1 x 2 ;B=x^ 2 +x^ 2 -x 1 ^ 2 x 2 ^ 2
Cho phương trình : x² - 2(m-3) x + m² +3 = 0.Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thoã mãn x1² + x2² = 86
Làm ơn giải chi tiết giúp từng bước giúp e với, e thật sự kh hiểu bài này, đây là bài thi ạ 🥺
Bài 1. Giải các phương trình sau:
1) \(\sqrt{2x-1}=\sqrt{5}\) 2) \(\sqrt{x-5}=3\) 3) \(\sqrt{9\left(x-1\right)}=21\) 4) \(\sqrt{2}x-\sqrt{50}=0\)
bài 1 giả bất phương trình
a, \(\frac{x-1}{x+3}\)>0
bài 2 giải bất phương trình
a, giá trị tuyệt đối x-5 >2
giúp mình với tối đi học rồi
Bài 2. Giải các phương trình sau. a) 3x - 2sqrt(x - 1) = 4 b) sqrt(4x + 1) - sqrt(x + 2) = sqrt(3 - x) c) (sqrt(x - 1) - sqrt(5 - x))(|10 - x| + 2x - 16) = 0
không giải phương trình dùng hệ thức vi-et hãy tính tổng và tích các nghiệm của mỗi phương trìh sau :
a)m\(^2\) -2(m+1)x+m+2=0(m≠0)
b) (2-\(\sqrt{3}\)) x\(^2\) +4x+2+\(\sqrt{2}\)=0
c)4x\(^2\)+2x=5=0
d)x\(^2\)-(1+\(\sqrt{2}\))x+\(\sqrt{2}\)