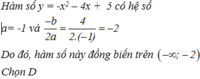Các câu hỏi tương tự
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
Câu 48. Cho y|x+1|+|x−2|và các mệnh đề 1)Hàm số tăng lên trên(-1,+∞)2)Hàm số không đổi trên[−1;2)3) Hàm số giảm trên(-∞,-1)4) Hàm số giảm trên (-2,+∞)Hỏi có bao nhiêu mệnh đề đúng?A. 0 B. 1 C. 2 D. 3Câu 49. Hàm số y-√|2x+3|nghịch biến trên khoảng.A.(-dfrac{3}{2},+infty)B.(-∞,-dfrac{3}{2})C. RD.Cả 3 đáp án đều sai
Đọc tiếp
Câu 48. Cho y=|x+1|+|x−2|và các mệnh đề
1)Hàm số tăng lên trên(-1,+∞)
2)Hàm số không đổi trên[−1;2)
3) Hàm số giảm trên(-∞,-1)
4) Hàm số giảm trên (-2,+∞)
Hỏi có bao nhiêu mệnh đề đúng?
A. 0 B. 1 C. 2 D. 3
Câu 49. Hàm số y=-√|2x+3|nghịch biến trên khoảng.
A.(\(-\dfrac{3}{2},+\infty\))
B.(-∞,\(-\dfrac{3}{2}\))
C. R
D.Cả 3 đáp án đều sai
Câu 48. Cho y=|x+1|+|x−2||x+1|+|x−2|và các mệnh đề
Câu 49. Hàm số y=-√|2x+3||2x+3| nghịch biến trên khoảng.
Câu 50. Hàm số y = 2 là hàm số gì.
A. Đồng biến B. Nghịch biến
C. không đồng biến cũng không nghịch biến D. Đáp án khác
Cho hàm số f(x) 4-3x. Khẳng định nào sau đây đúng: A. Hàm số nghịch biến trên left(frac{4}{3};+inftyright) B. Hàm số đồng biến trên ℝ C. Hàm số đồng biến trên left(frac{3}{4};+inftyright) C. Hàm số đồng biến trên left(-infty;frac{4}{3}right)
Đọc tiếp
Cho hàm số f(x) = 4-3x. Khẳng định nào sau đây đúng:
A. Hàm số nghịch biến trên \(\left(\frac{4}{3};+\infty\right)\) B. Hàm số đồng biến trên \(ℝ\)
C. Hàm số đồng biến trên \(\left(\frac{3}{4};+\infty\right)\) C. Hàm số đồng biến trên \(\left(-\infty;\frac{4}{3}\right)\)
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
C/m hàm số: y = x3 - x2 + x - 5 đồng biến trên miền xác định
có bao nhiêu giá trị nguyên của m trên (-4;4) để hàm số y=(m+2)x^2-3mx-5 đồng biến trên (3;+∞)
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
y = - 1 1 + x trên (-3; 2) và (2; 3)
Cho hai hàm số f(x) và g(x) cùng đồng biến trên khoảng (a; b). Có thể kết luận gì về chiều biến thiên của hàm số y = f(x) + g(x) trên khoảng (a; b)?
A. Đồng biến
B. Nghịch biến
C. Không đổi.
D. Không kết luận được.