Chọn B
Phương pháp: Dùng kiến thức cực đại cực tiểu của hàm số
Cách giải:
Nhìn vào đồ thị, ta thấy hàm số đạt cực tiểu tại điểm có tọa độ (0; 3)
Chọn B
Phương pháp: Dùng kiến thức cực đại cực tiểu của hàm số
Cách giải:
Nhìn vào đồ thị, ta thấy hàm số đạt cực tiểu tại điểm có tọa độ (0; 3)
Cho hàm số y=f(x) xác định, liên tục trên khoảng ( - ∞ ; + ∞ ) và có đồ thị là đường cong trong hình vẽ bên. Hàm số y=f(x) đạt cực tiểu tại điểm nào dưới đây
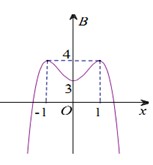
A. x=-1
B. x=0
C. x=1
D. x=+1, x=-1
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-4;0] và có đồ thị là đường cong trong hình bên. Hàm số f(x) đạt giá trị cực tiểu tại điểm nào dưới đây?
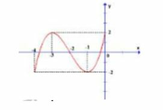
A. x = -1
B. x = -3
C. x = 2
D. x = -2
Cho hàm số y=f(x) xác định, liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây ?
A. x = -1
B. x = 1
C. y = 0
D. x = 0
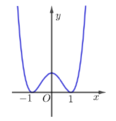
Cho hàm số y=f(x) xác định, liên tục trên đoạn [−2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?
A.x=-2
B.x=-1
C.x=1
D.x=2
Cho hàm số y=f(x) xác định và liên tục trên [-2;2] và có đồ thị là đường cong trong hình vẽ bên.
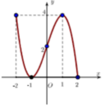
Hàm số f(x) đạt cực tiểu tại điểm
A.x=1
B.x=-2
C.x=2
D.x=-1
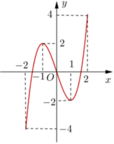
Cho hàm số y=f(x) xác định, liên tục trên R và có đồ thị là đường cong như hình vẽ. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?
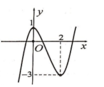
A. x=-3
B. x=1
C. x=0
D. x=2
Cho hàm số y=f(x) xác định, liên tục trên khoảng ( - ∞ ; 1 ) và ( 1 ; + ∞ ) , có đồ thị là đường cong trong hình vẽ bên. Đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng nào dưới đây
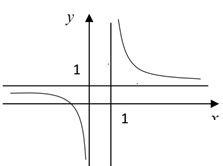
A. x=2
B. x=0
C. x=1
D. y=1
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hàm số g(x)=f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu?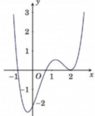
A. 3
B. 2
C. 1.
D. 4
Cho hàm số y = f(x) xác định, liên tục trên đoạn [a;b] (a < b) và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) có bao nhiêu điểm cực trị?
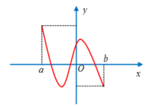
A. 1
B. 2
C. 3
D. 4