Đáp án B
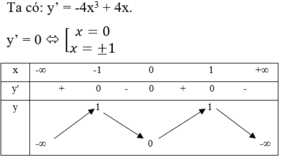
Từ bảng biến thiên suy ra y’ < 0 <=> x (-1; 0) (1; +∞) => Hàm số nghịch biến trên các khoảng (-1; 0); (1; +∞)
Đáp án B

Từ bảng biến thiên suy ra y’ < 0 <=> x (-1; 0) (1; +∞) => Hàm số nghịch biến trên các khoảng (-1; 0); (1; +∞)
Trong hai hàm số f(x) = x 4 + 2 x 2 + 1 và g(x) = x x + 1 . Hàm số nào nghịch biến trên khoảng ?
A. Không có hàm số nào cả.
B. Chỉ g(x)
C. Cả f(x), g(x)
D. Chỉ f(x)
Khoảng nghịch biến của hàm số y = x 4 - 2 x 2 - 1 là:
A. (-∞; -1) và (0; 1)
B. (-∞; 0) và (1; +∞)
C. (-∞; -1) ∪ (0; 1)
D. (0;1)
Cho hàm số y = x 4 - 2 x 2 + 1 . Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị;
2) Hàm số đồng biến trên các khoảng - 1 ; 0 ; 1 ; + ∞
3) Hàm số có 1 điểm cực trị;
4) Hàm số nghịch biến trên các khoảng - ∞ ; - 1 ; 0 ; 1
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2
B. 1
C. 4
D. 3
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
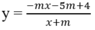
A. m < 1 hoặc m > 4 B. 0 < m < 1
C. m > 4 D. 1 ≤ m ≤ 4
Các khoảng nghịch biến của hàm số y = -1/4.x4 + 2x2 -5 là
A. (-2; 0) và (2; +∞).
B. (-1; 0) và (1 ; +∞)
C. (-∞; -2) và (0 ; 2).
D. (-∞; -1) và (1; +∞)
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
y = - mx - 5 m + 4 x + m
A. m < 1 hoặc m > 4 B. 0 < m < 1
C. m > 4 D. 1 ≤ m ≤ 4
Chứng minh rằng hàm số y = 2 x - x 2 đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Hàm số y = x4 – 2x2 – 1 đồng biến trên khoảng nào sau đây:
A. (-∞; -1) và (0; 1)
B. (-1; 0) và (0; 1)
C. (-1;0) và (1; +∞)
D. Đồng biến trên R
Hàm số y = - x 4 2 + 1 đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).