Các câu hỏi tương tự
Cho hàm số
f
x
x
3
+
a
x
2
+
b
x
+
c
thỏa mãn
c
2019
,
a
+
b
+
c
-
2018
0
. Số điểm cực trị của hàm số
y
f
x...
Đọc tiếp
Cho hàm số f x = x 3 + a x 2 + b x + c thỏa mãn c > 2019 , a + b + c - 2018 < 0 . Số điểm cực trị của hàm số y = f x - 2019 là
![]()
![]()
![]()
![]()
cho hàm số y=f(x) có f'(x) = (x-2021)^5 * (x-2020)^2020 * (x-2019)^2019. Hàm số f(x) có bao nhiêu điểm cực trị ?
Cho hàm số y = f ( x ) có đạo hàm trên R là f ' ( x ) = ( x - 2018 ) ( x - 2019 ) ( x - 2020 ) 4 . Hàm số đã cho có bao nhiêu điểm cực trị?
A. 2
B. 1
C. 4
D. 3
Cho hàm số f(x)= x(x-1)(x-2) (x-3)... (x-2019).
Tính f'(2019)
A. 2018!
B. 2019!
C. 1
D. 2019
Cho hàm số f(x)
x
(
x
-
1
)
(
x
-
2
)
.
.
.
(
x
-
2019
)
. Giá trị...
Đọc tiếp
Cho hàm số f(x)= x ( x - 1 ) ( x - 2 ) . . . ( x - 2019 ) . Giá trị của f'(0) là
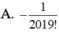
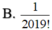
![]()
![]()
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019; 2019) để hàm số sau có tập xác định là D R
y
x
+
m
+
x
2
+
2
(
m
+
1
)
x
+
m
2
+
2...
Đọc tiếp
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019; 2019) để hàm số sau có tập xác định là D = R
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
Hàm số y = x 4 - x 3 - x + 2019 có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 0
D. 1
Cho hàm số
y
x
5
5
-
(
2
m
-
1
)
x
4
-
m
3
x
3
+
2019
. Có bao nhiêu giá trị của tham số m để hàm số đạt cực tiểu tại x 0? A. Vô số . B. 1. C. 2 . D. 0 .
Đọc tiếp
Cho hàm số y = x 5 5 - ( 2 m - 1 ) x 4 - m 3 x 3 + 2019 . Có bao nhiêu giá trị của tham số m để hàm số đạt cực tiểu tại x = 0?
A. Vô số .
B. 1.
C. 2 .
D. 0 .
Cho hàm số f(x)= x(x+1)(x+2) (x+3)... (x+2019).
Tính f'(0)
A. 2018!
B. 2019!
C. 0
D. 1
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
-
1
(
a
,
b
∈
ℝ
)
. Đồ thị của hàm số yf(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 0 là: A. 4 B. 0 C. 3 D. 2
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
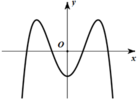
A. 4
B. 0
C. 3
D. 2




