Chọn D.
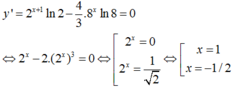
Xét y(-1) = 5/6 ; y(-1/2) = 0,9428; y(0) = 2/3
Suy ra ymin = 2/3
Chọn D.
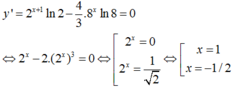
Xét y(-1) = 5/6 ; y(-1/2) = 0,9428; y(0) = 2/3
Suy ra ymin = 2/3
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho bài toán: “Xét tính đơn điệu của hàm số y = x 2 + 2 x - 3 ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định: D = ℝ \ ( - 3 ; 1 )
Bước 2: Tìm đạo hàm: y ' = x 2 + 2 x - 3 ' 2 x 2 + 2 x - 3 = x + 1 x 2 + 2 x - 3
Bước 3: y ' = 0 ⇔ x + 1 = 0 x 2 + 2 x - 3 > 0 ⇔ x = 1 x < - 3 ⇔ x ∈ ∅ ; x > 1
Bước 4: Bảng biến thiên:
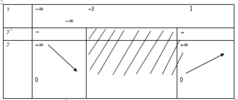
Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng ( - ∞ ; - 3 ] , đồng biến trên nửa khoảng [ 1 ; + ∞ ) . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5
Cho hàm số f(x) có đạo hàmf'(x) xác định và liên tục trên đoạn [0;6]. Đồ thị hàm số y=f'(x) như hình vẽ bên. Biết f(0)=f(3)=f(6)=-1,f(1)=f(5)=1. Số điểm cực trị của hàm số y = [ f ( x ) ] 2 trên đoạn [0;6] là
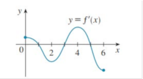
A. 5.
B. 7.
C. 9.
D. 8.
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Gọi M, m lần lượt là GTLN, GTNN của hàm số f(x) = (x2 – 3)ex trên đoạn [0; 2]. Giá trị biểu thức A = (m2 – 4M)2016 bằng:
A. 1
B. 22016
C. 0
D. e2016
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5