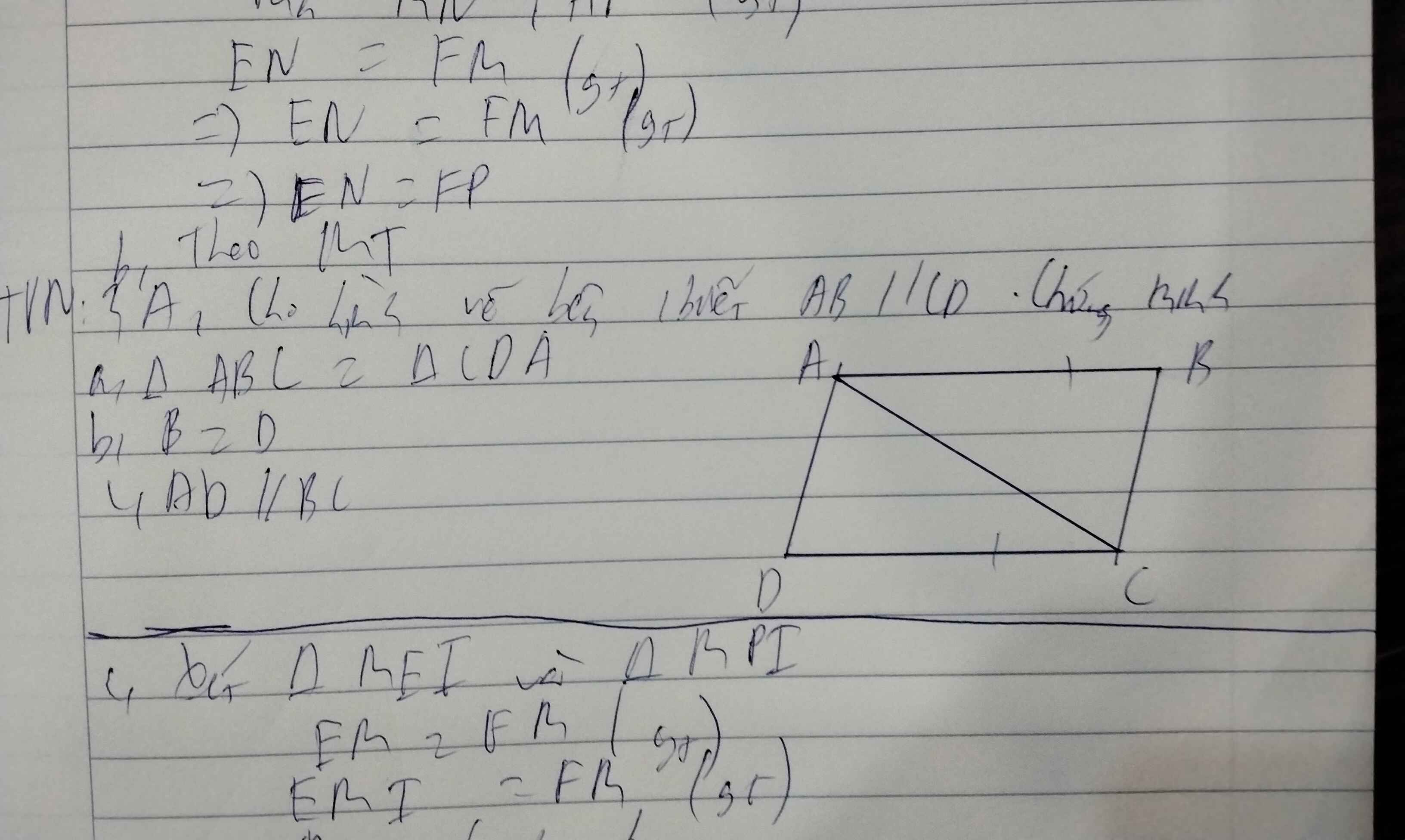Question

  gt tôi với mai thi xin đó

Answer 1

a.

Do \(AB||CD\Rightarrow\widehat{BAC}=\widehat{DCA}\) (so le trong)

Xét hai tam giác ABC và tam giác CDA có:

\(\left\{{}\begin{matrix}AB=CD\left(gt\right)\\\widehat{BAC}=\widehat{DCA}\left(cmt\right)\\AC\text{ là cạnh chung}\end{matrix}\right.\)

\(\Rightarrow\Delta ABC=\Delta CDA\left(c.g.c\right)\)

b.

Từ câu a, do \(\Delta ABC=\Delta CDA\Rightarrow\widehat{B}=\widehat{D}\)

c.

Cũng từ câu a, do \(\Delta ABC=\Delta CDA\Rightarrow\widehat{ACB}=\widehat{CAD}\)

Mà \(\widehat{ACB}\) và \(\widehat{CAD}\) là hai góc ở vị trí so le trong

\(\Rightarrow AD||BC\)