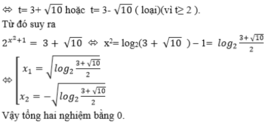Các câu hỏi tương tự
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Biết rằng phương trình
l
o
g
2
3
x
-
(
m
+
2
)
l
o
g
3
x
+
3
m
-
1
0
có hai nghiệm
x
1
,
x
2
thảo mãn
x
1...
Đọc tiếp
Biết rằng phương trình l o g 2 3 x - ( m + 2 ) l o g 3 x + 3 m - 1 = 0 có hai nghiệm x 1 , x 2 thảo mãn x 1 . x 2 = 27 . Khi đó tổng x 1 + x 2 bằng
A. 6
B. 12
C. 1 3
D. 34 3
Với tất cả giá trị nào của tham số m thì phương trình
(
m
-
10
)
x
2
-
2
(
m
-
2
)
x
+
m
-
3
0
có hai nghiệm
x
1
,
x
2
thỏa mãn
x
1
+
x...
Đọc tiếp
Với tất cả giá trị nào của tham số m thì phương trình ( m - 10 ) x 2 - 2 ( m - 2 ) x + m - 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 + x 1 . x 2 < 1
A. 1<m<3.
B. 1<m<2.
C. m>2.
D. m>3.
Gọi
x
1
,
x
2
là 2 nghiệm của phương trình
4
x
+
1
-
5
.
2
x
+
1
+
4
0
. Khi đó giá trị
S
x
1
+...
Đọc tiếp
Gọi x 1 , x 2 là 2 nghiệm của phương trình 4 x + 1 - 5 . 2 x + 1 + 4 = 0 . Khi đó giá trị S = x 1 + x 2 là
A. -1
B. 0
C. 1
D. 2
Gọi
x
1
,
x
2
là 2 nghiệm của phương trình
4
x
+
1
-
5
.
2
x
+
1
+
4
0
. Khi đó giá trị
S
...
Đọc tiếp
Gọi x 1 , x 2 là 2 nghiệm của phương trình 4 x + 1 - 5 . 2 x + 1 + 4 = 0 . Khi đó giá trị S = x 1 + x 2 là
A.-1
B.0
C.1
D.2
Biết rằng phương trình
log
3
2
x
-
(
m
+
2
)
log
3
x
+
3
m
-
1
0
có hai nghiệm
x
1
,
x
2
thỏa mãn
x
1
x
2
27
. Khi đó tổng
x...
Đọc tiếp
Biết rằng phương trình log 3 2 x - ( m + 2 ) log 3 x + 3 m - 1 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 x 2 = 27 . Khi đó tổng x 1 + x 2 bằng
A. 6
B. 12
C.![]()
D. ![]()
Gọi x1, x2 là 2 nghiệm của phương trình
2
-
3
x
+
2
+
3
x
4
Khi đó...
Đọc tiếp
Gọi x1, x2 là 2 nghiệm của phương trình 2 - 3 x + 2 + 3 x = 4 Khi đó x 1 2 + 2 x 2 2 bằng
A.2
B. 5
C. 4
D. 3
Giá trị của tham số m để phương trình
4
x
-
m
.
2
(
x
+
1
)
+
2
m
0
có 2 nghiệm
x
1
,
x
2
thỏa mãn
x
1
+
x...
Đọc tiếp
Giá trị của tham số m để phương trình 4 x - m . 2 ( x + 1 ) + 2 m = 0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 là
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Biết rằng phương trình
log
2
x
-
15
.
log
x
2
2
có hai nghiệm
x
1
,
x
2
x
1
x
2...
Đọc tiếp
Biết rằng phương trình log 2 x - 15 . log x 2 = 2 có hai nghiệm x 1 , x 2 x 1 > x 2 . Giá trị của x 1 - 16 x 2 bằng
A. - 4095 8
B. 34
C. 30
D. 4097 8