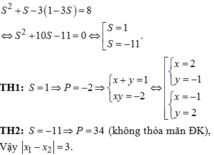Các câu hỏi tương tự
Hệ phương trình:
x
+
y
+
2
y
-
1
+
x
-
y
5...
Đọc tiếp
Hệ phương trình: x + y + 2 y - 1 + x - y = 5 y 2 + 2 = x y + y có cặp nghiệm duy nhất (x;y). Tính x + 3y.
A. 2
B. 4
C. 5
D. 7
Gọi (x;y) là nghiệm dương của hệ phương trình
x
+
y
+
x
-
y
4
x
2
+...
Đọc tiếp
Gọi (x;y) là nghiệm dương của hệ phương trình x + y + x - y = 4 x 2 + y 2 = 128 .Tổng x+y bằng
A. 12
B. 8
C. 16
D. 0
Cho đồ thị hàm số y f (x) như hình vẽ.Phương trình
x
+
2
(
x
-
1
)
2
có đúng 2 nghiệm phân biệt khi và chỉ khi: A.
m
0
m...
Đọc tiếp
Cho đồ thị hàm số y = f (x) như hình vẽ.
Phương trình x + 2 ( x - 1 ) 2 có đúng 2 nghiệm phân biệt khi và chỉ khi:
A. m < 0 m = 4
B. 0 ≤ m ≤ 4
C. m > 4 m = 0
D. m = 0 m = - 4
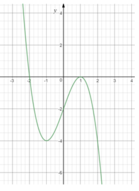
Cho hàm số yf(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số yf(x) và yf(x) . Phương trình f(x)
m
e
x
có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ? A. 0,27. B. −0,54. C. −0,27. D. 0,54.
Đọc tiếp
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.
Hình vẽ dưới đây là đồ thị của hàm số
y
3
x
-
2
x
-
1
. Tìm tất cả các giá trị thực của tham số m để phương trình
3
x
-
2
x
-...
Đọc tiếp
Hình vẽ dưới đây là đồ thị của hàm số y = 3 x - 2 x - 1 . Tìm tất cả các giá trị thực của tham số m để phương trình 3 x - 2 x - 1 = m có hai nghiệm phân biệt?
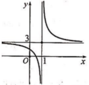
A. -3 < m < 0
B. m < -3
C. 0 < m < 3
D. m > 3
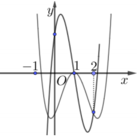
Cho hàm số yf(x) có đồ thị trong hình bên. Phương trình f(x)1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2? A. 1. B. 2. C. 3. D. 0.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị trong hình bên. Phương trình f(x)=1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2?

A. 1.
B. 2.
C. 3.
D. 0.
Cho hàm số yf(x) xác định, liên tục trên R và có bảng biến thiên sau.Tập hợp các giá trị m để phương trình f(x)m+2 có hai nghiệm phân biệt là A.
(
2
;
+
∞
)
B.
R
∖
{
-
2
}
C.
(
-
2
;
+
∞
)
∪
{
-
3
}
D. (-3;-2)
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau.
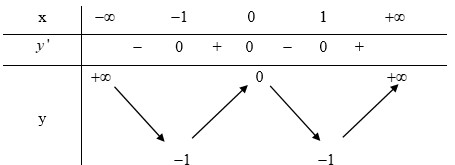
Tập hợp các giá trị m để phương trình f(x)=m+2 có hai nghiệm phân biệt là
A. ( 2 ; + ∞ )
B. R ∖ { - 2 }
C. ( - 2 ; + ∞ ) ∪ { - 3 }
D. (-3;-2)
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng
∆
:
x
-
2
1
y
-
1
1
z
-
2
và vuông góc với mặt phẳng (β):x+y+2z+10. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng ∆ : x - 2 1 = y - 1 1 = z - 2 và vuông góc với mặt phẳng (β):x+y+2z+1=0. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình
A. x - 1 = y + 1 1 = z - 1
B. x 1 = y + 1 1 = z - 1 1
C. x - 2 1 = y + 1 - 5 = z 2
D. x + 2 1 = y - 1 - 5 = z 2
Cho hàm số
y
f
(
x
)
liên tục trên
ℝ
và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau(1) Hàm số
y
f
(
x
)
đạt cực đại tại
x
0
0
(2) Hàm số
y
f
(
x
)
có ba cực trị.(3) Phương trình
y
f
(
x
)
có đúng ba nghiệm phân biệt(4) Hàm...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2