Các câu hỏi tương tự
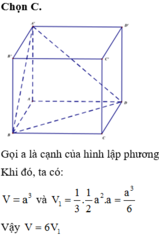
Gọi V là thể tích hình lập phương ABCD.A’B’C’D’,
V
1
là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng A. V 6
V
1
B. V 4
V
1
C. V 3
V
1
D. V 2
V
1
Đọc tiếp
Gọi V là thể tích hình lập phương ABCD.A’B’C’D’, V 1 là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng
A. V= 6 V 1
B. V= 4 V 1
C. V= 3 V 1
D. V= 2 V 1
Gọi V là thể tích khối lập phương
A
B
C
D
.
A
B
C
D
,
V
là thể tích khối tứ diện
A
.
A
B
D
Hệ thức nào dưới đây là đúng ? A.
V
4
V
B.
V
8
V
C.
V...
Đọc tiếp
Gọi V là thể tích khối lập phương A B C D . A ' B ' C ' D ' , V ' là thể tích khối tứ diện A ' . A B D Hệ thức nào dưới đây là đúng ?
A. V = 4 V '
B. V = 8 V '
C. V = 6 V '
D. V = 2 V '
Cho (H) là hình phẳng giới hạn bởi các đường
y
e
x
, trục tung, trục hoành và đường thẳng x 1. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox. Khẳng định nào sau đây là đúng về thể tích V? A.
V
π
2
e
2
B.
V
π
2
e
-...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi các đường y = e x , trục tung, trục hoành và đường thẳng x = 1. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox. Khẳng định nào sau đây là đúng về thể tích V?
A. V = π 2 e 2
B. V = π 2 e - 1
C. V = 1 2 e 2 - 1
D. V = π 2 e 2 - 1
Cho khối tứ diện ABCD. Gọi M, N lần luợt là trung điểm của AB và CD (tham khảo hình vẽ bên). Đặt V là thể tích của khối tứ diện ABCD, là thể tích của khối tứ diện MNBC. Khẳng định nào sau đây đúng? A.
V
1
V
1
4
B.
V
1
V
1...
Đọc tiếp
Cho khối tứ diện ABCD. Gọi M, N lần luợt là trung điểm của AB và CD (tham khảo hình vẽ bên). Đặt V là thể tích của khối tứ diện ABCD, là thể tích của khối tứ diện MNBC. Khẳng định nào sau đây đúng?
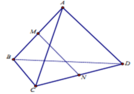
A. V 1 V = 1 4
B. V 1 V = 1 2
C. V 1 V = 1 3
D. V 1 V = 2 3
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ABa,A’2a. Biết thể tích hình cầu ngoại tiếptứ diện ABCD’ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A’B’C’D’ A.
2
a
3
3
B.
2
a
3
C.
4
a...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a,A’=2a. Biết thể tích hình cầu ngoại tiếp
tứ diện ABCD’ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A’B’C’D’
A. 2 a 3 3
B. 2 a 3
C. 4 a 3
D. 4 a 3 3
Cho tứ diện ABCD có thể tích V. Gọi
A
1
B
1
C
1
D
1
là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích
V
1
. Gọi
A
2
B
2
C
2
D
2...
Đọc tiếp
Cho tứ diện ABCD có thể tích V. Gọi A 1 B 1 C 1 D 1 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích V 1 . Gọi A 2 B 2 C 2 D 2 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác B 1 C 1 D 1 , C 1 D 1 A 1 , D 1 A 1 B 1 , A 1 B 1 C 1 và có thể tích V 2 … cứ như vậy cho tứ diện A n B n C n D n có thể tích V n với n là số tự nhiên lớn hơn 1. Tính giá trị của biểu thức P = lim n → + ∞ V + V 1 + ... + V n .
A. 27 26 V
B. 1 27 V
C. 9 8 V
D. 82 81 V
Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD. A.
2
V
3
B.
2
V
5
C.
V
3
D.
V
6
Đọc tiếp
Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD.
A. 2 V 3
B. 2 V 5
C. V 3
D. V 6
Gọi V là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có phương trình x 2 25 + y 2 16 = 1 . V có giá trị gần nhất với giá trị nào sau đây?
A. 550
B. 400
C. 670
D. 335
Gọi R là bán kính, S là diện tích và V là thể tích của khối cầu. Công thức nào sau đây là sai? A.
S
π
R
2
B.
S
4
π
R
2
C.
V
4
3
π
R
3
D.
3
V
S...
Đọc tiếp
Gọi R là bán kính, S là diện tích và V là thể tích của khối cầu. Công thức nào sau đây là sai?
A. S = π R 2
B. S = 4 π R 2
C. V = 4 3 π R 3
D. 3 V = S . R