Chọn B.
Phương pháp:
Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp.
Cách giải:
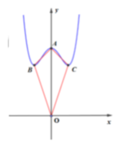


Khi đó,
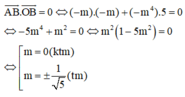
Vậy tập hợp S tất cả các giá trị của tham số m thỏa mãn yêu cầu đề bài có 2 phần tử là ± 1 5 .
Chọn B.
Phương pháp:
Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp.
Cách giải:



Khi đó,
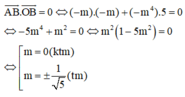
Vậy tập hợp S tất cả các giá trị của tham số m thỏa mãn yêu cầu đề bài có 2 phần tử là ± 1 5 .
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số 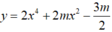 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
![]()
B. -3
C. -1
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 + 2 m x 2 − 3 m 2 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S
A. 2 − 2 3
B. − 2 − 2 3
C. − 1
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 + 2 m x 2 − 3 m 2 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
A. 2 − 2 3 .
B. − 2 − 3 .
C. -1.
D. 0.
Tìm tập hợp S tất cả các giá trị của tham số m để đồ thị hàm số y = x 4 − 2 m 2 x 2 + m 4 + 3 có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành tứ giác nội tiếp
A. S = − 1 3 ; 0 ; 1 3
B. S = − 1 ; 1
C. S = − 1 3 ; 1 3
D. S = − 1 2 ; 1 2
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m 2 x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2/3
C. 1.
D. 5.
Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A, B, C sao cho OA=BC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng
A. 8
B. -8
C. 4
C. -4
Tìm các giá trị của tham số m để đồ thị hàm số y = x 4 − 2 m 2 x 2 + m 4 + 1 có ba điểm cực trị. Đồng thời ba điểm cực trị đó cùng với gốc O tạo thành một tứ giác nội tiếp.
A. m = ± 1
B. m = -1
C. m = 1
D. không tồn tại m
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m 2 + 2 có ba điểm cực trị cùng với điểm D(2;1) tạo thành một tứ giác nội tiếp được đường tròn?
A. 0
B. 2
C. 3.
D. 1