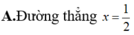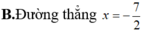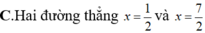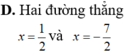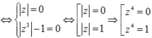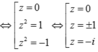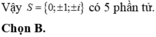Các câu hỏi tương tự
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.
z
¯
1 và |z -
3
+ i|. Tìm số phần tử của S A. 1. B. 2. C. 3. D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Gọi S là tập hợp các số thực m sao cho với mỗi
m
∈
S
có đúng một số phức thỏa mãn
z
-
m
6
và
z
z
-
4
là số thuần ảo. Tính tổng c...
Đọc tiếp
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 và z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 10
B. 0
C. 16
D. 8
Gọi S là tập hợp các số thực m sao cho với mỗi m
∈
S có đúng một số phức thỏa mãn
z
-
m
6
v
à
z
z
-
4
là số thuần ảo. Tính tổng của các phần tử của tập S
Đọc tiếp
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 v à z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt
z
1
,
z
2
thỏa mãn đồng thời các phương trình
z
-
1
z
-
i
và
z
+
2
m
m...
Đọc tiếp
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần thực của z là số đối của phần ảo của nó
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng.
B. Đường tròn.
C. Một điểm xác định.
D. Elip.
Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của z nằm trong đoạn [-1;3] là: A. Các điểm nằm trong phần giới hạn bởi đường thẳng x -1 và x 3, kể cả biên. B. Các điểm nằm trong phần giới hạn bởi đường thẳng x -1 và x 3, không kể biên. C. Các điểm nằm trong phần giới hạn bởi đường thẳng y -1 và y 3, không kể biên. D. Các điểm nằm trong phần giới hạn bởi đường thẳng y -1 và y 3, kể cả biên.
Đọc tiếp
Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của z nằm trong đoạn [-1;3] là:
A. Các điểm nằm trong phần giới hạn bởi đường thẳng x = -1 và x = 3, kể cả biên.
B. Các điểm nằm trong phần giới hạn bởi đường thẳng x = -1 và x = 3, không kể biên.
C. Các điểm nằm trong phần giới hạn bởi đường thẳng y = -1 và y = 3, không kể biên.
D. Các điểm nằm trong phần giới hạn bởi đường thẳng y = -1 và y = 3, kể cả biên.
Gọi S là tập hợp các số phức thỏa mãn
z
-
3
+
z
+
3
10
Gọi z1, z2 là hai số phức S có mô đun nhỏ nhất. Giá trị biểu thức
P
z
1
2
+
z
2
2
là
Đọc tiếp
Gọi S là tập hợp các số phức thỏa mãn z - 3 + z + 3 = 10 Gọi z1, z2 là hai số phức S có mô đun nhỏ nhất. Giá trị biểu thức P = z 1 2 + z 2 2 là
![]()
![]()
![]()
![]()
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
z
+
z
¯
+
3
4
là
Đọc tiếp
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z + z ¯ + 3 = 4 là