Các câu hỏi tương tự
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
-
1
x
+
1
và các trục tọa độ. Khi đó giá trị của S bằng A. S ln2 - 1 (đvdt) B. S 2ln2 - 1 (đvdt) C. S 2ln2 + 1 (đvdt) D. S ln2 + 1 (đvdt)
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x - 1 x + 1 và các trục tọa độ. Khi đó giá trị của S bằng
A. S = ln2 - 1 (đvdt)
B. S = 2ln2 - 1 (đvdt)
C. S = 2ln2 + 1 (đvdt)
D. S = ln2 + 1 (đvdt)
Cho hàm số
y
x
-
m
2
x
+
1
(với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. Hai. B. Ba. C. Một. D. Không
Đọc tiếp
Cho hàm số y = x - m 2 x + 1 (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. Hai.
B. Ba.
C. Một.
D. Không
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
x
2
+
1
trục Ox và đường thẳng x1 bằng
a
b
-
ln
1
+
b...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 x 2 + 1 trục Ox và đường thẳng x=1 bằng a b - ln 1 + b c với a,b,c là các nguyên số dương. Khi đó giá trị của a+b+c là:
A. 11.
B. 12.
C. 13.
D. 14.
Cho hàm số bậc ba yf(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng...
Đọc tiếp
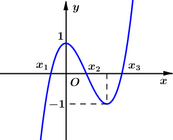
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số
y
x
4
+
x
2
, trục hoành, trục tung và đường thẳng x 1. Biết
S
a
5
+
b
,
a
,
b
∈
ℚ
. Tính a + b A.
a
+...
Đọc tiếp
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 + x 2 , trục hoành, trục tung và đường thẳng x = 1. Biết S = a 5 + b , a , b ∈ ℚ . Tính a + b
A. a + b = - 1
B. a + b = 1 2
C. a + b = 1 3
D. a + b = 13 3
Giả sử
S
a
ln
b
c
-
1
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
+
1
x
-
2
với các trục tọa độ. Hỏi mệnh đề nào là đúng?
Đọc tiếp
Giả sử S = a ln b c - 1 là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x + 1 x - 2 với các trục tọa độ. Hỏi mệnh đề nào là đúng?
![]()
![]()
![]()
![]()
Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số
y
x
và
y
e
x
, trục tung và đường thẳng x1 được tính theo công thức
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x và y = e x , trục tung và đường thẳng x=1 được tính theo công thức
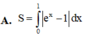
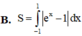
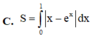
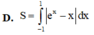
Cho đồ thị (C) của hàm số
y
x
3
-
3
x
2
+
1
. Gọi (d) là tiếp tuyến của (C) tại điểm A có hoành độ
x
A
a
. Biết diện tích hình phẳng giới hạn bởi (d) và (C) bằng , các giá trị của a thỏa mãn đẳng thức nào? A. . B. . C. . D. .
Đọc tiếp
Cho đồ thị (C) của hàm số
y
=
x
3
-
3
x
2
+
1
. Gọi (d) là tiếp tuyến của (C) tại điểm A có hoành độ
x
A
=
a
. Biết diện tích hình phẳng giới hạn bởi (d) và (C) bằng ![]() , các giá trị của a thỏa mãn đẳng thức nào?
, các giá trị của a thỏa mãn đẳng thức nào?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y
x
e
x
và các đường thẳng x 1, x 2, y 0. Thể tích của khối tròn xoay thu được khi quay hình D xung quanh trục Ox bằng
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x = 1, x = 2, y = 0. Thể tích của khối tròn xoay thu được khi quay hình D xung quanh trục Ox bằng
![]()
![]()
![]()




