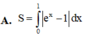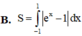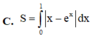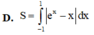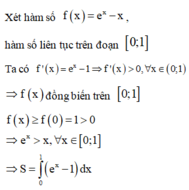Các câu hỏi tương tự
Cho hàm số f(x) liên tục trên R diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
f
(
x
)
trục hoành và hai đường thẳng xa;xb (ab) được tính theo công thức
Đọc tiếp
Cho hàm số f(x) liên tục trên R diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ) trục hoành và hai đường thẳng x=a;x=b (a<b) được tính theo công thức
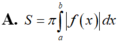
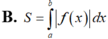
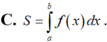
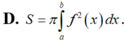
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y f(x) trục hoành và hai đường thẳng xa; xb (ab) được tính theo công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b (a<b) được tính theo công thức:
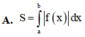
![]()
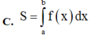
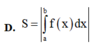
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng x a và x b được tính theo công thức nào dưới đây ?
Đọc tiếp
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y =f(x) trục hoành và hai đường thẳng x = a và x =b được tính theo công thức nào dưới đây ?
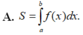
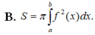
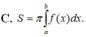
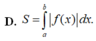
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
y
f
1
(
x
)
,
y
f
2
(
x
)
liên tục và hai đường thẳng
x
a
,
x
b
được tính theo công thức: A.
S
∫...
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f 1 ( x ) , y = f 2 ( x ) liên tục và hai đường thẳng x = a , x = b được tính theo công thức:
A. S = ∫ a b f 1 x - f 2 x d x
B. S = ∫ a b f 1 x - f 2 x d x
C. S = ∫ a b f 1 x - f 2 x d x
D. S = ∫ a b f 1 x - ∫ a b f 2 x d x
Cho hàm số y f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y f(x), trục hoành và hai đường thẳng x a; x b được tính theo công thức
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức
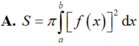
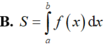
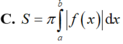

Cho hai hàm số y f(x) và y g(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x a; x b Diện tích S của hình phẳng D được tính theo công thức
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a; x = b Diện tích S của hình phẳng D được tính theo công thức
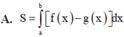
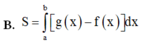
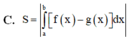
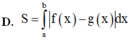
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x , trục tung, trục hoành và đường thẳng x=1 là:
A. 1
B. 2
C. 1 2
D. 3 2
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y4-
1
x
2
(x0) đường thẳng y-1,đường thẳng y1 và trục tung được diện tích như sau:
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=4- 1 x 2 (x>0) đường thẳng y=-1,đường thẳng y=1 và trục tung được diện tích như sau:
![]()
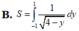
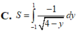
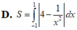
Diện tích hình phẳng được giới hạn bởi đồ thi hàm số y ex – e–x, trục hoành, trục tung và đường thẳng x –1, x 1 là: A.
2
e
+
1
e
-
2
B.
2
e
-
1
e...
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đồ thi hàm số y = ex – e–x, trục hoành, trục tung và đường thẳng x = –1, x = 1 là:
A. 2 e + 1 e - 2
B. 2 e - 1 e - 2
C. 2 e + 1 e + 2
D. 2 e - 1 e - 1