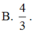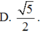Các câu hỏi tương tự
Tứ diện ABCD là tứ diện đều nội tiếp trong mặt cầu bán kính R. Tính độ dài của cạnh tứ diện đều theo R A. R
2
B. R
3
C.
2
R
2
3
D.
R
6
2
Đọc tiếp
Tứ diện ABCD là tứ diện đều nội tiếp trong mặt cầu bán kính R. Tính độ dài của cạnh tứ diện đều theo R
A. R 2
B. R 3
C. 2 R 2 3
D. R 6 2
Gọi l và R lần lượt là tổng độ dài các cạnh và bán kính mặt cầu ngoại tiếp một tứ diện. Hỏi rằng trong số các tứ diện, tứ diện nào thì tỉ số
l
R
đạt giá trị lớn nhất. Tính giá trị lớn nhất đó?
Đọc tiếp
Gọi l và R lần lượt là tổng độ dài các cạnh và bán kính mặt cầu ngoại tiếp một tứ diện. Hỏi rằng trong số các tứ diện, tứ diện nào thì tỉ số l R đạt giá trị lớn nhất. Tính giá trị lớn nhất đó?
![]()
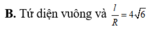

![]()
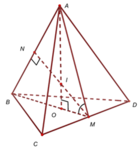
Tứ diện đều ABCD nội tiếp trong mặt cầu bán kính R. Tính AB theo R
A. AB = R 8 3
B. AB = R 3
C. AB = 3 R 2
D. AB = 4 R 3
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a
2
Đọc tiếp
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
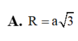
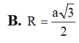
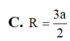
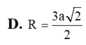
Tứ diện đều ABCD nội tiếp trong mặt cầu bán kính R. Tính độ dài AB.
A. AB = R 8 3
B. AB = R 3
C. AB = R 2
D. AB = 3 R 2
Cho tứ diện ABCD. Gọi
h
A
,
h
B
,
h
C
,
h
D
lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ di...
Đọc tiếp
Cho tứ diện ABCD. Gọi h A , h B , h C , h D lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng: 1 h A + 1 h B + 1 h C + 1 h D = 1 r
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2
,
...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu S 1 , S 2 , S 3 . Khẳng định nào sau đây đúng?
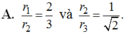
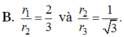
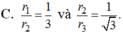
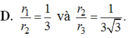
Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD với AB=2a
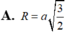
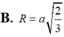
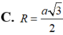
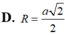
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là: A. I(2; -1; 0); R 2
3
B. I(4; -3; -2); R 4
3
C. I(3; -2; -1); R 3
3
D. I(3; -2; -1); R 9
Đọc tiếp
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2 3
B. I(4; -3; -2); R = 4 3
C. I(3; -2; -1); R = 3 3
D. I(3; -2; -1); R = 9