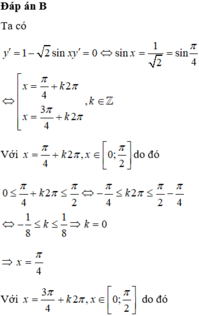Các câu hỏi tương tự
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
sin
x
+
c
os
2
x
trên đoạn
0
;
π
.
Khi đó
2
M
+
m
bằng A. 4 B.
5
2
C.
7
2
D. 5
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + c os 2 x trên đoạn 0 ; π . Khi đó 2 M + m bằng
A. 4
B. 5 2
C. 7 2
D. 5
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
f
x
sin
x
1
+
cos
x
trên đoạn
0
;
π
A.
M
3
3
2
;
m
1
B.
M...
Đọc tiếp
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = sin x 1 + cos x trên đoạn 0 ; π
A. M = 3 3 2 ; m = 1
B. M = 3 3 4 ; m = 0
C. M = 3 3 ; m = 1
D. M = 3 ; m = 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
(
x
)
2
c
o
s
3
x
-
c
o
s
2
x
trên đoạn D[
-
π
/
3
;
π
/
3
] A.
m
a
x
(
x
∈...
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 c o s 3 x - c o s 2 x trên đoạn D=[ - π / 3 ; π / 3 ]
A. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
B. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = - 3
C. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = - 3
D. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
s
inx+
cos
2
x
+
sin
3
x
trên đoạn
0
;
π
. Tính P M + m A.
P
16
27
B.
P
−
19
+
13...
Đọc tiếp
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = s inx+ cos 2 x + sin 3 x trên đoạn 0 ; π . Tính P = M + m
A. P = 16 27
B. P = − 19 + 13 13 27
C. P = − 19 − 13 13 27
D. P = − 16 27
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
x
3
+
2
x
2
-
x
+
2
trên đoạn
-
1
;
1
2
. Khi đó tích số M.m bằng A.
45
4
B. ...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - x 3 + 2 x 2 - x + 2 trên đoạn - 1 ; 1 2 . Khi đó tích số M.m bằng
A. 45 4
B. 212 47
C. 125 36
D. 100 9
Có tất cả bao nhiêu giá trị nguyên của tham số m Î [-20;20] để hàm số
y
8
c
o
t
x
+
m
-
3
.
2
c
o
t
x
+
3
m
-
2
đồng biến trên khoảng (π/4;π)? A....
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m Î [-20;20] để hàm số y = 8 c o t x + m - 3 . 2 c o t x + 3 m - 2 đồng biến trên khoảng (π/4;π)?
A. 10
B. 12
C. 11
D. 9
Cho hàm số
f
(
x
)
1
+
c
o
s
x
(
x
-
π
)...
Đọc tiếp
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm giá trị lớn nhất của hàm số y = x + sin 2 x trên đoạn [ 0 ; π ]
A. π
B. 0
C. 3 π 4 + 1 2
D. 3 π 4
Tìm giá trị lớn nhất của hàm số
y
x
+
cos
2
x
trên đoạn
0
;
π
A.
m
a
x
0
;
π
y
3
π
+...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = x + cos 2 x trên đoạn 0 ; π
A. m a x 0 ; π y = 3 π + 2 4
B. m a x 0 ; π y = π + 1
C. m a x 0 ; π y = π - 2 4
D. m a x 0 ; π y = π + 2 4