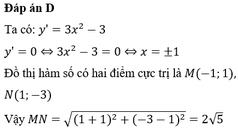Các câu hỏi tương tự
Gọi M, N là các điểm cực tiểu của đồ thị hàm số y = 1 4 x 4 - 8 x 2 + 3 . Độ dài đoạn thẳng MN bằng
A. 10
B. 6
C. 8
D. 4
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
. Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN A.
M
N
4
2
B. MN 3 C.
M
N
2
2...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN
A. M N = 4 2
B. MN = 3
C. M N = 2 2
D. M N = 3 5
Khi đồ thị hàm số
y
x
3
-
3
m
x
+
2
có hai điểm cực trị A, B và đường tròn (C):
(
x
-
1
)
2
+
(
y
-
1
)
2
3
cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN A. MN...
Đọc tiếp
Khi đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A, B và đường tròn (C): ( x - 1 ) 2 + ( y - 1 ) 2 = 3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN
A. MN= 3
B. MN=1.
C. MN=2.
D. MN=2 3
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
.
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.
I
0
;
-...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)
Cho đồ thị hàm số
y
1
3
x
4
-
2
x
2
-
1
có ba điểm cực trị là A, B, C. Biết M, N là hai điểm di động lần lượt thuộc các cạnh AB, AC sao cho diện tích tam giác ABC gấp ba lần diện tích tam giác AMN. Giá trị nhỏ nhất của độ dài đoạn thẳng MN là A..
2
3
B.
2...
Đọc tiếp
Cho đồ thị hàm số y = 1 3 x 4 - 2 x 2 - 1 có ba điểm cực trị là A, B, C. Biết M, N là hai điểm di động lần lượt thuộc các cạnh AB, AC sao cho diện tích tam giác ABC gấp ba lần diện tích tam giác AMN. Giá trị nhỏ nhất của độ dài đoạn thẳng MN là
A.. 2 3
B. 2 3 3
C. 4
D. 2
Cho đồ thị hàm số
y
9
8
x
4
-
3
x
2
-
1
có ba điểm cực trị A, B, C như hình vẽ. Biết M, N lần lượt thuộc AB, AC sao cho đoạn thẳng MN chia tam giác ABC thành hai phần bằng nhau. Giá trị nhỏ nhất của MN là A.
2
6
3...
Đọc tiếp
Cho đồ thị hàm số y = 9 8 x 4 - 3 x 2 - 1 có ba điểm cực trị A, B, C như hình vẽ. Biết M, N lần lượt thuộc AB, AC sao cho đoạn thẳng MN chia tam giác ABC thành hai phần bằng nhau. Giá trị nhỏ nhất của MN là
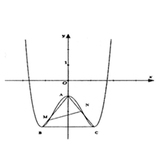
A. 2 6 3
B. 2 2 3
C. 2 5 3
D. 2 7 3
Gọi M;N là giao điểm của đồ thị hàm số và đường thẳng
y
x
+
2
. Khi đó tung độ trung điểm I của đoạn MN bằng bao nhiêu? A.
−
3
2
B.
11
2
C.
7
2
D.
−
7
2
Đọc tiếp
Gọi M;N là giao điểm của đồ thị hàm số và đường thẳng y = x + 2 . Khi đó tung độ trung điểm I của đoạn MN bằng bao nhiêu?
A. − 3 2
B. 11 2
C. 7 2
D. − 7 2
Gọi M, N là các giao điểm của đường thẳng
y
x
−
4
với đồ thị của hàm số
y
−
2
x
+
5
x
−
2
. Tìm tọa độ trung điểm I của MN? A.
I
2
;
−
2...
Đọc tiếp
Gọi M, N là các giao điểm của đường thẳng y = x − 4 với đồ thị của hàm số y = − 2 x + 5 x − 2 . Tìm tọa độ trung điểm I của MN?
A. I 2 ; − 2
B. I 1 ; − 3
C. I 3 ; − 1
D. I − 2 ; 2
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 − 2 x 2 + 2 v à y = − x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)