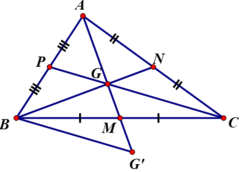
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC
Theo tính chất đường trung tuyến của tam giác ta có:
GB = 2/3.BN (1)
GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)
GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = G'M .
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
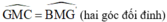
MC = MB
⇒ ΔGMC = ΔG’MB (c.g.c)
⇒ GC = G’B (hai cạnh tương ứng).
Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)
Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.











