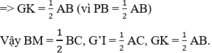Gọi I, K lần lượt là trung điểm của BG, BG’.
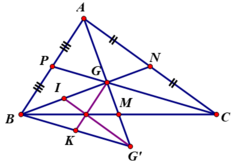
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
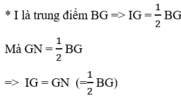
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
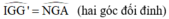
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
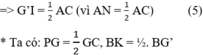
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)

Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
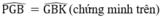
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)