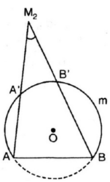
Điểm M 2 là điểm nằm ngòi đường tròn
Gọi M 2 A v à M 2 B là góc có đỉnh nằm ngoài đường tròn nên:
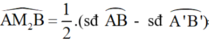

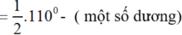
![]()

Điểm M 2 là điểm nằm ngòi đường tròn
Gọi M 2 A v à M 2 B là góc có đỉnh nằm ngoài đường tròn nên:
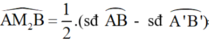

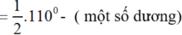
![]()
Gọi cung chứa góc 55o ở bài tập 46 là cung AmB. Lấy điểm M1 nằm bên trong và điểm M2 nằm bên ngoài đường tròn chứa cung này sao cho M1, M2 và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:
A M 1 B ^ > 55 o
Gọi cung chứa góc 55 ° ở bài tập 46 là cung AmB. Lấy điểm M1 nằm bên trong và điểm M2 nằm bên ngoài đường tròn chứa cung này sao cho M1, M2 và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:
a ) A M 1 B ^ > 55 0 b ) A M 2 B ^ < 55 °
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
cho đường (o) và điểm M bên ngoài đường tròn.Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (A,B là tiếp điểm) a) chứng minh tứ giác MAOB nội tiếp b) Biết góc AMB = 40 độ .Tính số đo góc ở tâm góc AOB và số đo cung nhỏ AB? Số đo cung lớn AB
Cho đường tròn (O) và tam ABC nội tiếp đường tròn sao cho B A C ^ = 30 0 . Trên cung AC –không chứa điểm B lấy điểm D sao cho A C D ^ = 30 0 , AC cắt BD tại M nằm trong đường tròn. Tính số đo góc A M B ^
A. 120 °
B. 60 °
C. 150 °
D. 165 °
Cho đường tròn (O;3) điểm M nằm bên ngoài đg tròn .Qua M kẻ tiếp tuyến MA,MB với đg tròn (A,B thuộc đg tròn sao cho góc AMB=60°) a, ∆AMB là hình gì ?VS? b. Qua C trên cung nhỏ AB kẻ tiếp tuyến vs đg tròn cắt MA,MB lần lượt tại N và Q .Tính góc NOQ c. Tính chu vi ∆MNQ
Bài 1. Cho hình chữ nhật ABCD, M là một điểm bất kì thỏa mãn AMB ̂ =900
. Chứng minh rằng MA2 + MB2 + MC2 + MD2 không đổi
Bài 2. Cho đường tròn (O,R), P là điểm cố định nằm trong đường tròn.
Qua P kẻ 2 dây cung AB và CD vuông góc với nhau.
1) Chứng minh PA2 + PB2 + PC2 + PD2 không đổi
2) Gọi M là trung điểm của AC. Chứng minh PM vuông góc với BD
Cho đường tròn tâm O đường kính AB. Trên cùng một nửa đường tròn (O) đường kính AB lấy hai điểm C, D sao cho cung AC nhỏ hơn cung AD. Gọi T là giao điểm của hai đường thẳng CD và AB. Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằm trên nửa đường tròn tâm O chứa điểm C). Gọi E là giao điểm của MN và AB. Chứng minh rằng:
1. TM là tiếp tuyến của (O).
2. TM2 = TC. TD
3. 4 điểm O, D, C, E cùng nằm trên một đường tròn.
(mình cần câu 3 thôi)
bài 1 :Cho điểm M thuộc nửa đường tròn đường kính AB (M khác A và B). Lấy điểm I nằm giữa M và B, kẻ IH vuông góc với AB tại H. Đoạn thẳng AI cắt đoạn thẳng MH tại K. Chứng minh rằng ![]()
bài 2 : Cho đường tròn (O), từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC (B, C là hai tiếp điểm). Gọi M là giao điểm của OA và BC, D là một điểm nằm trên đường tròn (O) sao cho D không nằm trên đường thẳng OA, kẻ dây cung DE đi qua M. Chứng minh tứ giác ADOE nội tiếp.