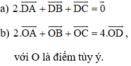Các câu hỏi tương tự
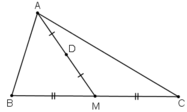
Bài 4. Cho tam giác ABC có AM là đường trung tuyến và D là trung điểm của AM. a) Chứng minh rằng: 2 vec DA + vec DB + vec DC = vec 0 b) Chứng minh rằng: vec BD = 1 2 vec B vec A + 1 4 vec BC . c) Gọi E là điểm trên cạnh AC sao cho AE = 1/3 * A * C Chứng minh rằng B, D, E thẳng hàng. Tính tỉ số (DB)/(DE)
Gọi AM là trung tuyến của tam giác ABC; D là trung điểm của đoạn AM và điểm O tùy ý. Chứng minh rằng:
- 2DA + DB + DC = 0
- 2OA + OB + OC = 4OD
Gọi AM là trung tuyến của tam giác ABC; D là trung điểm của đoạn AM và điểm O tùy ý. Chứng minh rằng:
- 2DA + DB + DC = 0
- 2OA + OB + OC = 4OD
Gọi CM là trung tuyến của tam giác ABC và D là trung điểm của CM . Đẳng thức nào sau đây đúng?
Đọc tiếp
Gọi CM là trung tuyến của tam giác ABC và D là trung điểm của CM . Đẳng thức nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho tam giác ABC có trung tuyến AM, D là trung điểm của AM. Đẳng thức nào sau đây là sai? A.
2
D
A
→
+
D
B
→
+
D
C
→
0
→
B.
D...
Đọc tiếp
Cho tam giác ABC có trung tuyến AM, D là trung điểm của AM. Đẳng thức nào sau đây là sai?
A. 2 D A → + D B → + D C → = 0 →
B. D A → + D B → + D C → = 0 →
C. 2 O A → + O B → + O C → = 4 O D → với mọi điểm O
D. M A → + M B → + M C → = 2 M D →
Trong tam giác vuông ABC kẻ đường cao CK từ đỉnh của góc vuông C, còn trong △ACK kẻ đường phân giác CE. Gọi D là trung điểm của đoạn AC và F là giao điểm của các đường thẳng DE và CK. Chứng minh rằng BF//CE.
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với ABAC. Đường phân giác của góc
B
A
C
^
cắt (O) tại điểm D khác A Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O. Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC. Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.
Cho tam giác ABC có trung tuyến AM, gọi I là trung điểm AM. Đẳng thức nào sau đây đúng? A. B. C. D.
Đọc tiếp
Cho tam giác ABC có trung tuyến AM, gọi I là trung điểm AM. Đẳng thức nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng