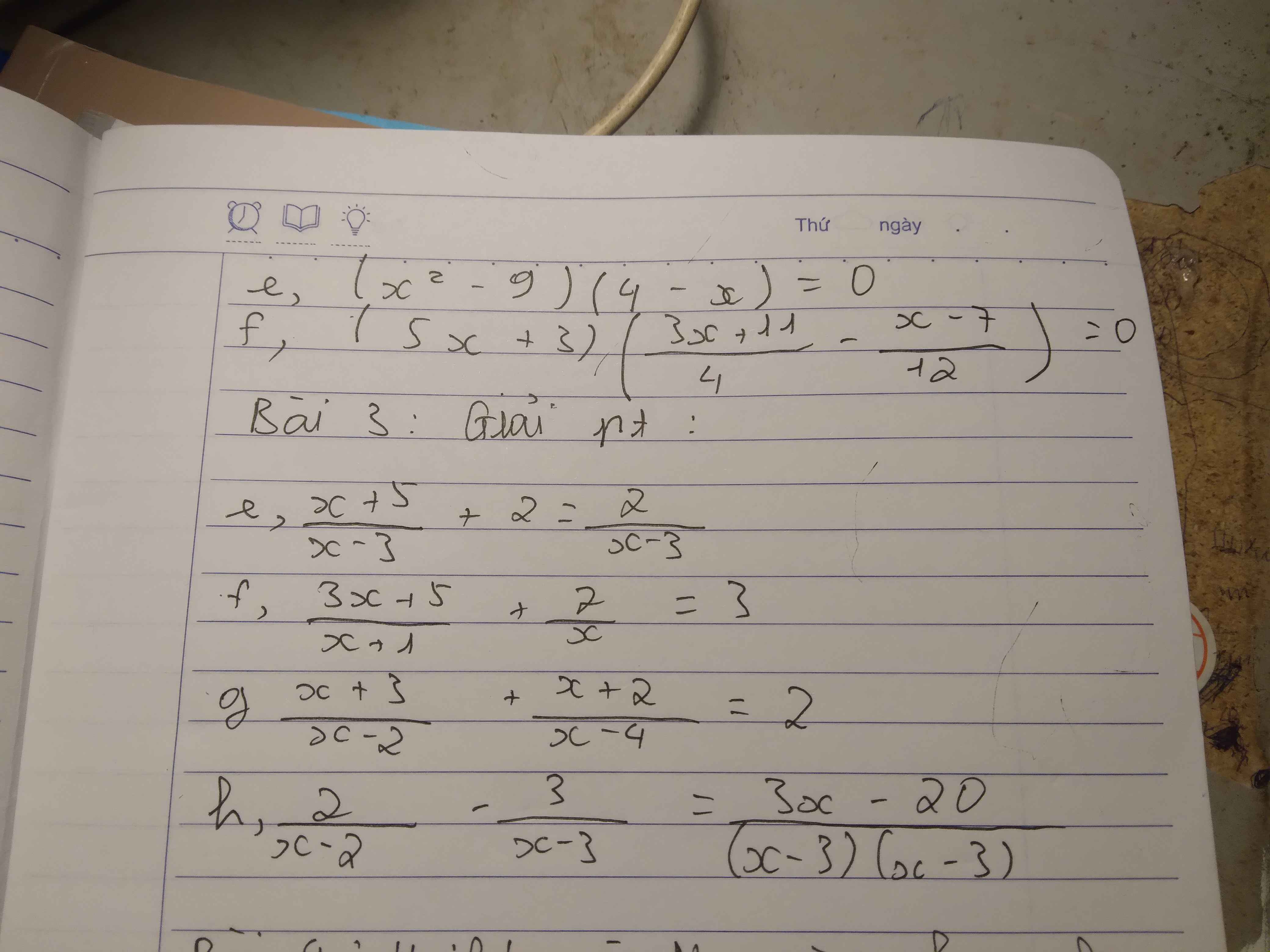e: \(\left(x^2-9\right)\left(4-x\right)=0\)
=>(x-3)(x+3)(4-x)=0
=>\(\left[{}\begin{matrix}x-3=0\\x+3=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x=4\end{matrix}\right.\)
f: \(\left(5x+3\right)\left(\dfrac{3x+11}{4}-\dfrac{x-7}{12}\right)=0\)
=>\(\left(5x+3\right)\cdot\dfrac{3\left(3x+11\right)-x+7}{12}=0\)
=>\(\left(5x+3\right)\left(9x+33-x+7\right)=0\)
=>\(\left(5x+3\right)\left(8x+40\right)=0\)
=>\(\left[{}\begin{matrix}5x+3=0\\8x+40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\x=-5\end{matrix}\right.\)
Bài 3:
e: ĐKXĐ: \(x\ne3\)
\(\dfrac{x+5}{x-3}+2=\dfrac{2}{x-3}\)
=>\(\dfrac{x+5+2\left(x-3\right)}{x-3}=\dfrac{2}{x-3}\)
=>x+5+2(x-3)=2
=>x+5+2x-6=2
=>3x-1=2
=>3x=3
=>x=1(nhận)
f: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(\dfrac{3x+5}{x+1}+\dfrac{7}{x}=3\)
=>\(\dfrac{x\left(3x+5\right)+7\left(x+1\right)}{x\left(x+1\right)}=3\)
=>\(3x\left(x+1\right)=x\left(3x+5\right)+7\left(x+1\right)\)
=>\(3x^2+3x=3x^2+5x+7x+7\)
=>12x+7=3x
=>9x=-7
=>\(x=-\dfrac{7}{9}\left(nhận\right)\)
g: ĐKXĐ: \(x\notin\left\{2;4\right\}\)
\(\dfrac{x+3}{x-2}+\dfrac{x+2}{x-4}=2\)
=>\(\dfrac{\left(x+3\right)\cdot\left(x-4\right)+\left(x+2\right)\left(x-2\right)}{\left(x-4\right)\left(x-2\right)}=2\)
=>\(2\left(x-4\right)\left(x-2\right)=\left(x+3\right)\left(x-4\right)+\left(x+2\right)\left(x-2\right)\)
=>\(2\left(x^2-6x+8\right)=x^2-4x+3x-12+x^2-4\)
=>\(2x^2-12x+16=2x^2-x-16\)
=>-12x+16=-x-16
=>-11x=-32
=>\(x=\dfrac{32}{11}\left(nhận\right)\)
h: ĐKXĐ: \(x\notin\left\{2;3\right\}\)
Sửa đề: \(\dfrac{2}{x-2}-\dfrac{3}{x-3}=\dfrac{3x-20}{\left(x-2\right)\left(x-3\right)}\)
=>\(\dfrac{2\left(x-3\right)-3\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{3x-20}{\left(x-2\right)\left(x-3\right)}\)
=>\(\dfrac{3x-20}{\left(x-2\right)\left(x-3\right)}=\dfrac{2x-6-3x+6}{\left(x-2\right)\left(x-3\right)}=\dfrac{-x}{\left(x-2\right)\left(x-3\right)}\)
=>3x-20=-x
=>3x+x=20
=>4x=20
=>x=5(nhận)