Question

;-; giúp vs

Answer 1

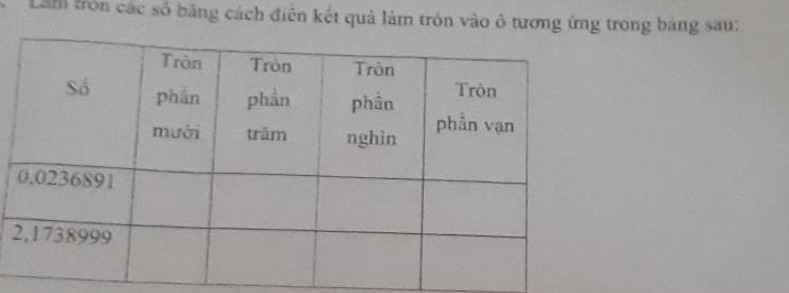
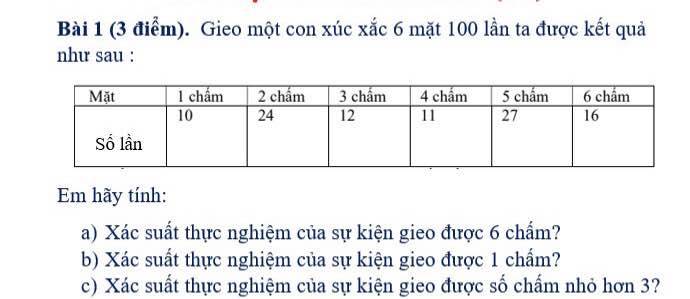
gọi số cần tìm lúc đầu là \(\overline{\text{aa}a}\) số chia lúc đầu là \(\overline{bbb}\) số dư lúc đầu là \(\overline{r}\) 

ta có: 

\(\overline{aaa}=2\cdot\overline{bbb}+r\\ \overline{aa}=2\cdot\overline{bb}+r-100\)

từ đó suy ra \(\overline{aaa}-\overline{aa}=2\cdot\left(\overline{bbb}\cdot\overline{bb}\right)+100\\ \Rightarrow\overline{a00}=2\cdot\overline{b00}+100\\ \Rightarrow a=2b+1\)

ta có bảng sau :

\(b\)	\(1\)	\(2\)	3	4
\(a\)	\(3\)	\(5\)	7	9

 

thử từng trường hợp , ta có 3 đáp số : 

\(555v\text{à}222;777v\text{à}333;999v\text{à}444\)