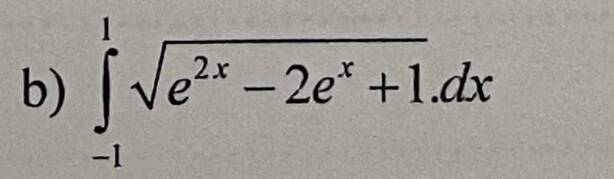70.
\(2^x>3^x\Leftrightarrow x.ln2>x.ln3\)
\(\Leftrightarrow x\left(ln3-ln2\right)< 0\)
\(\Leftrightarrow x< 0\)
71.
ĐKXĐ: \(\left\{{}\begin{matrix}3x-2>0\\6-5x>0\end{matrix}\right.\) \(\Rightarrow\dfrac{2}{3}< x< \dfrac{6}{5}\)
\(log_2\left(3x-2\right)>log_2\left(6-5x\right)\)
\(\Leftrightarrow3x-2>6-5x\)
\(\Leftrightarrow8x>8\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ ta được: \(1< x< \dfrac{6}{5}\)
72.
ĐKXĐ: \(x>0\)
\(log_2x+log_4x=3\)
\(\Leftrightarrow log_2x+\dfrac{1}{2}log_2x=3\)
\(\Leftrightarrow\dfrac{3}{2}log_2x=3\)
\(\Leftrightarrow log_2x=2\)
\(\Leftrightarrow x=4\)
73.
\(2^x+2^{x-1}+2^{x-2}=3^x-3^{x-1}+3^{x-2}\)
\(\Leftrightarrow2^x+\dfrac{1}{2}.2^x+\dfrac{1}{4}.2^x=3^x-\dfrac{1}{3}.3^x+\dfrac{1}{9}.3^x\)
\(\Leftrightarrow\dfrac{7}{4}.2^x=\dfrac{7}{9}.3^x\)
\(\Leftrightarrow2^{x-2}=3^{x-2}\)
\(\Leftrightarrow\left(x-2\right).ln2=\left(x-2\right).ln3\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
74.
\(2^{2x+6}+2^{x+7}=17\)
\(\Leftrightarrow\left(2^{x+3}\right)^2+16.2^{x+3}-17=0\)
Đặt \(2^{x+3}=t>0\Rightarrow t^2+16t-17=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-17\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow2^{x+3}=1\)
\(\Rightarrow x+3=0\)
\(\Rightarrow x=-3\)
75.
\(5^{x-1}+5^{3-x}=26\)
\(\Leftrightarrow5^{x-1}+25.5^{1-x}=26\)
Đặt \(5^{x-1}=t>0\)
\(\Rightarrow t+\dfrac{25}{t}=26\Rightarrow t^2-26t+25=0\Rightarrow\left[{}\begin{matrix}t=1\\t=25\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}5^{x-1}=1\\5^{x-1}=25\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-1=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
76.
\(3^x+4^x=5^x\)
\(\Leftrightarrow\left(\dfrac{3}{5}\right)^x+\left(\dfrac{4}{5}\right)^x-1=0\)
Xét hàm \(f\left(x\right)=\left(\dfrac{3}{5}\right)^x+\left(\dfrac{4}{5}\right)^x-1\)
\(f'\left(x\right)=\left(\dfrac{3}{5}\right)^x.ln\left(\dfrac{3}{5}\right)+\left(\dfrac{4}{5}\right)^x.ln\left(\dfrac{4}{5}\right)< 0;\forall x\)
\(\Rightarrow f\left(x\right)\) nghịch biến trên R
\(\Rightarrow f\left(x\right)=0\) có tối đa 1 nghiệm
Nhận thấy \(x=2\) là 1 nghiệm của pt đã cho
Vậy pt có nghiệm duy nhất \(x=2\)
77.
\(2^x=-x+6\Leftrightarrow2^x+x-6=0\)
Xét hàm \(f\left(x\right)=2^x+x-6\)
\(f'\left(x\right)=2^x.ln2+1>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow f\left(x\right)\) có tối đa 1 nghiệm
Nhận thấy \(x=2\) là 1 nghiệm của pt
Vậy pt có nghiệm duy nhất \(x=2\)
78.
\(4^x-2m.2^x+m+2=0\)
Đặt \(2^x=t>0\Rightarrow t^2-2mt+m+2=0\) (1)
Pt đã cho có 2 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m-2>0\\t_1+t_2=2m>0\\t_1t_2=m+2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\\m>0\\m>-2\end{matrix}\right.\)
\(\Rightarrow m>2\)
79.
ĐKXĐ: \(x>9\)
\(\log x+\log\left(x-9\right)=1\)
\(\Rightarrow\log x\left(x-9\right)=1\)
\(\Leftrightarrow x\left(x-9\right)=10\)
\(\Leftrightarrow x^2-9x-10=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-1\left(loại\right)\end{matrix}\right.\)
80.
ĐKXĐ: \(x>\dfrac{2}{3}\)
\(\ln x+\ln\left(3x-2\right)=0\)
\(\Rightarrow\ln x\left(3x-2\right)=0\)
\(\Rightarrow x\left(3x-2\right)=1\)
\(\Rightarrow3x^2-2x-1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho có đúng 1 nghiệm
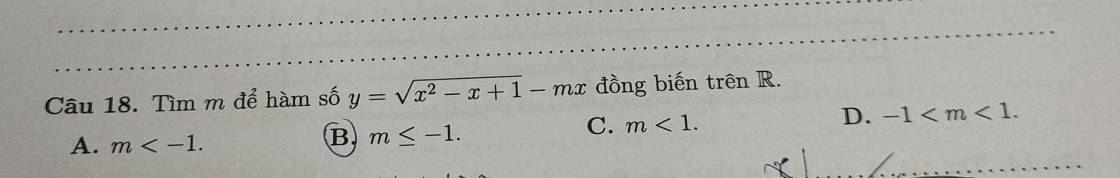
Giúp với
giúp mk với :(((((((((((
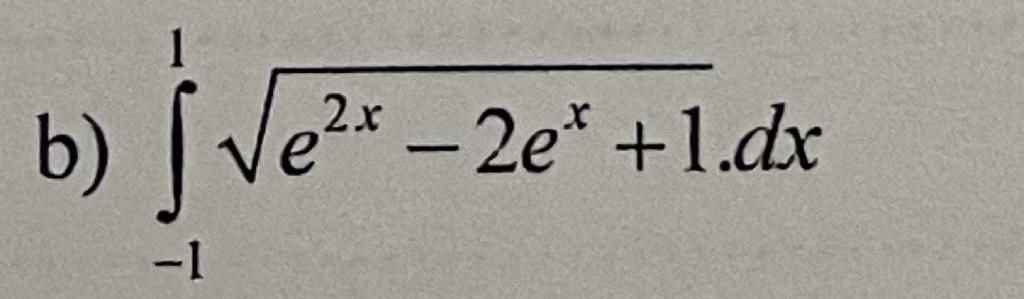giúp mik với
