\(a,\) Vì ABCD là hbh nên \(\widehat{A}=\widehat{C}=120^0\)
Mà AB//CD và ABCD là hbh nên \(\widehat{B}=\widehat{D}=180^0-\widehat{A}=60^0\)
\(b,\) Vì ABCD là hbh nên AD//BD do đó \(\widehat{C}+\widehat{D}=180^0\left(trong.cùng.phía\right)\)
Mà \(\widehat{C}-\widehat{D}=30^0\Rightarrow\left\{{}\begin{matrix}\widehat{C}=\left(180^0+30^0\right):2=105^0\\\widehat{D}=180^0-105^0=75^0\end{matrix}\right.\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=105^0\\\widehat{B}=\widehat{D}=75^0\end{matrix}\right.\)
\(c,\) Vì ABCD là hbh nên AD//BC do đó \(\widehat{A}+\widehat{B}=180^0\)
Ta có \(\widehat{A}:\widehat{B}=4:5\Rightarrow\dfrac{\widehat{A}}{4}=\dfrac{\widehat{B}}{5}\)
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{4}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{A}+\widehat{B}}{9}=\dfrac{180^0}{9}=20^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=80^0\\\widehat{B}=100^0\end{matrix}\right.\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=80^0\\\widehat{B}=\widehat{D}=100^0\end{matrix}\right.\)








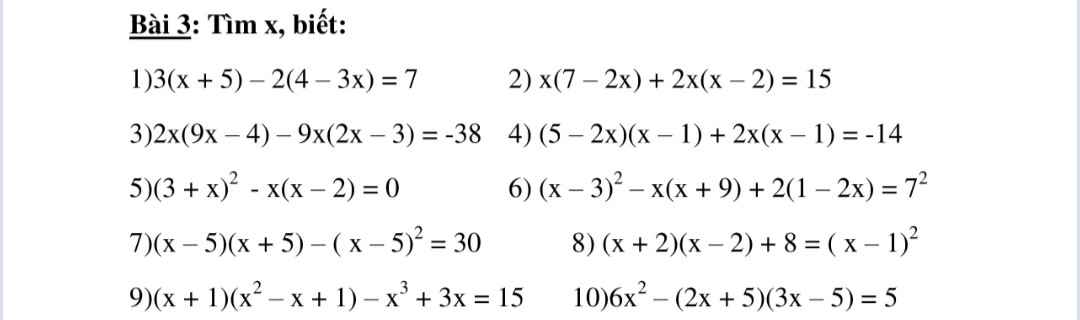


 giai pt giup minh voi a
giai pt giup minh voi a





 Giup mik voi
Giup mik voi