b)
\(\Delta=\left[-\left(m^2+3\right)\right]^2-4\cdot1\cdot\left(2m^2+2\right)=\left(m^2+3\right)^2-8m^2-8=m^4+6m^2+9-8m^2-8\)
\(=m^4-2m^2+1=\left(m^2-1\right)^2\)
PT có 2 nghiệm pb \(\Leftrightarrow\Delta>0\Leftrightarrow\left(m^2-1\right)^2>0\Leftrightarrow m^2-1\ne0\Leftrightarrow m^2\ne1\Leftrightarrow m\ne\pm1\)
Theo Vi-ét có \(\left\{{}\begin{matrix}x_1+x_2=m^2+3\\x_1x_2=2m^2+2\end{matrix}\right.\)
Theo đề bài \(\left\{{}\begin{matrix}x_1>1\\x_2>1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1-1>0\\x_2-1>0\end{matrix}\right.\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)>0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1>0\)
\(\Leftrightarrow2m^2+2-\left(m^2+3\right)+1>0\)
\(\Leftrightarrow m^2-1+1>0\)
\(\Leftrightarrow m^2>0\Leftrightarrow m\ne0\)
Kết hợp ĐK, \(m\ne\left\{-1;0;1\right\}\) thì PT(1) có 2 nghiệm pb lớn hơn 1

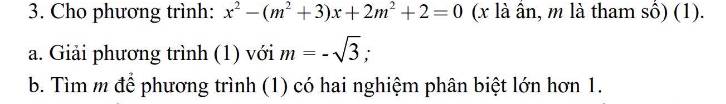 giúp tui phần b với đang cần gấp ạ
giúp tui phần b với đang cần gấp ạ





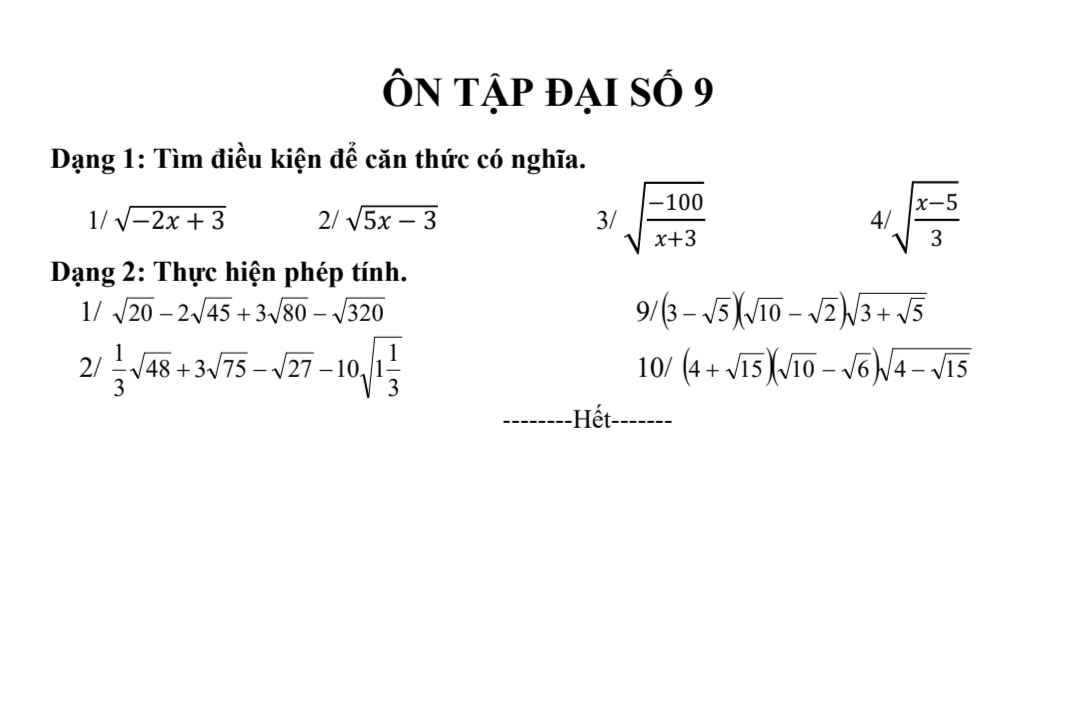

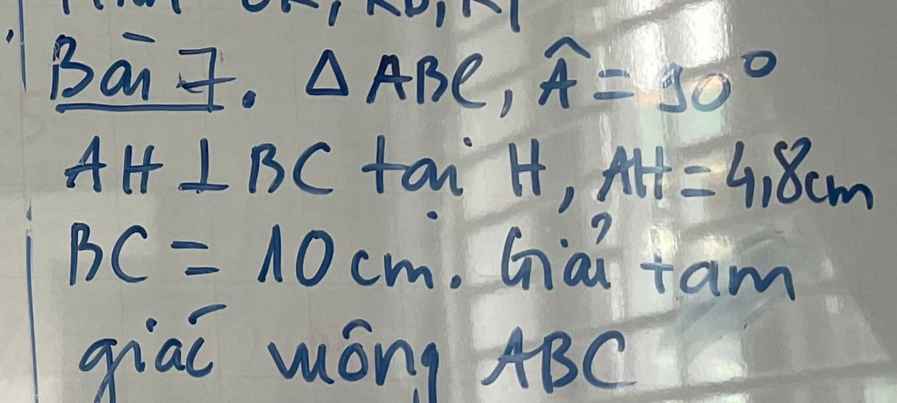












 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp