a: \(\left(9-4\sqrt{5}\right)\left(4\sqrt{5}+9\right)\)
\(=9^2-\left(4\sqrt{5}\right)^2\)
=81-80
=1
b: \(A=\left(\dfrac{\sqrt{x}+1}{x-4}-\dfrac{\sqrt{x}-1}{x+4\sqrt{x}+4}\right)\cdot\dfrac{x\sqrt{x}+2x-4\sqrt{x}-8}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+2\right)^2}\right)\cdot\dfrac{x\left(\sqrt{x}+2\right)-4\left(\sqrt{x}+2\right)}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)^2}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(x-4\right)}{\sqrt{x}}\)
\(=\dfrac{x+3\sqrt{x}+2-x+3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{6\sqrt{x}}{\sqrt{x}}=6\)
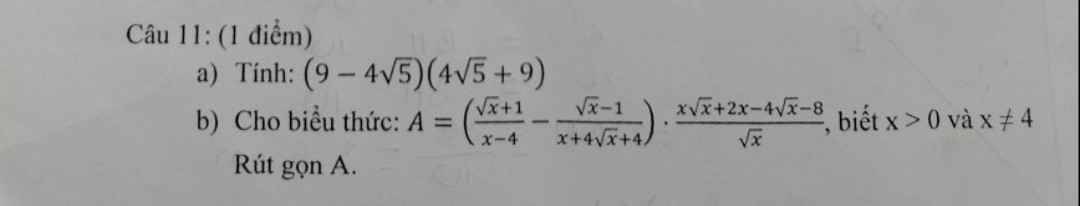
Giải giúp tớ với ạ, tớ cần gấp lắm
