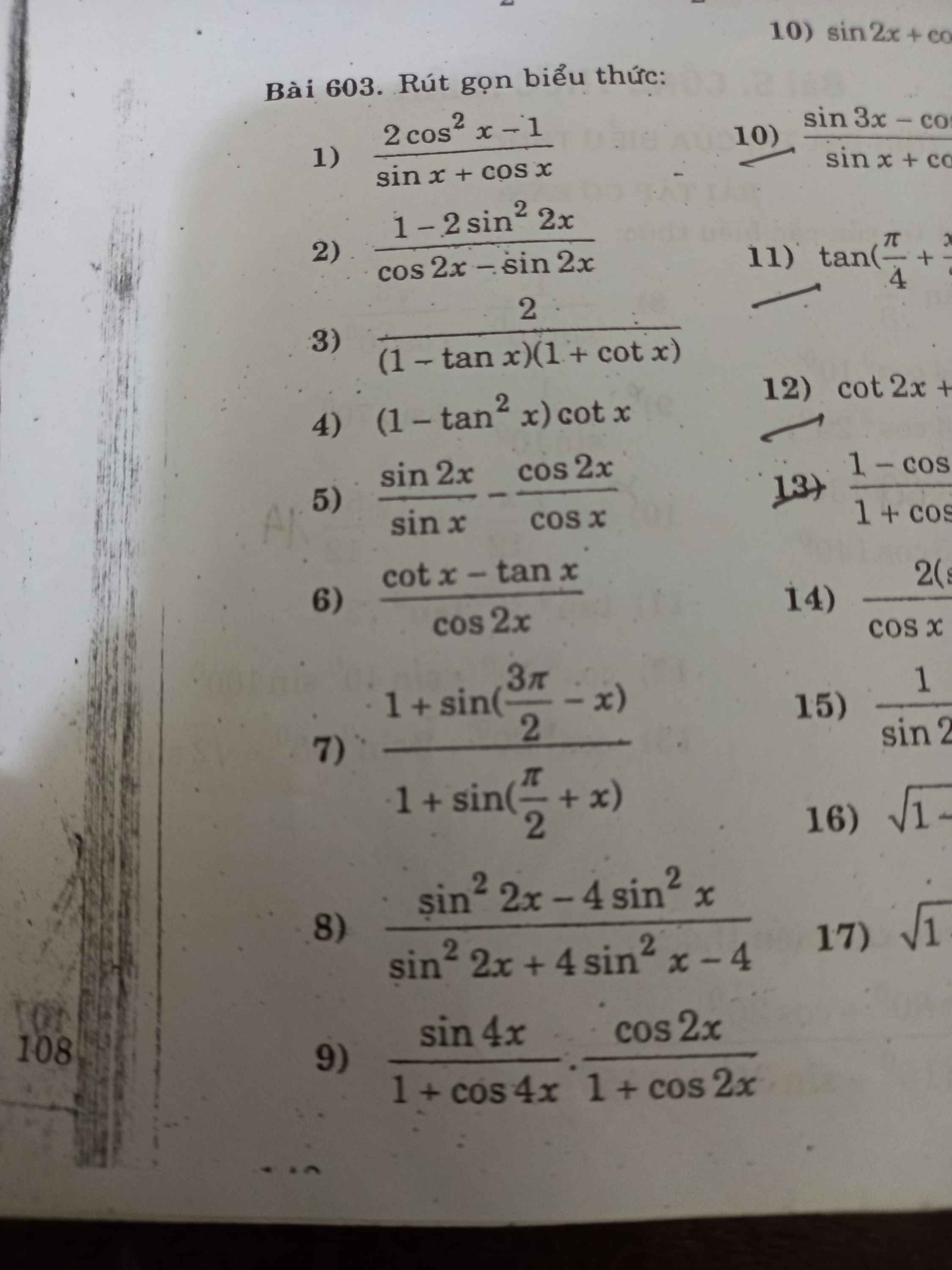Câu 16: Xét ΔABC có \(cosB=\dfrac{a^2+c^2-b^2}{2ac}=\dfrac{13^2+15^2-14^2}{2\cdot13\cdot15}=\dfrac{33}{65}\)
nên \(\widehat{B}\simeq59^029'\)
=>Chọn C
Câu 15: Xét ΔABC có \(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{13^2+15^2-24^2}{2\cdot13\cdot15}=\dfrac{-182}{390}\)
=>\(\widehat{A}\simeq117^049'\)
=>Chọn B
Câu 14: Xét ΔABC có \(cosA=\dfrac{b^2+c^2-a^2}{2bc}\)
=>\(b^2+c^2-a^2=2bc\cdot cosA\)
=>\(2\cdot bc\cdot cosA=\sqrt{3}bc\)
=>\(cosA=\dfrac{\sqrt{3}}{2}\)
=>\(\widehat{A}=30^0\)
=>Chọn A
Câu 12: Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{4^2+9^2-7^2}{2\cdot4\cdot9}=\dfrac{16+81-49}{8\cdot9}=\dfrac{48}{72}=\dfrac{2}{3}\)
=>Chọn D
Câu 11: \(a^2+c^2-b^2-2ac=\left(a-c\right)^2-b^2=\left(a-c-b\right)\left(a-c+b\right)\)
Vì a,b,c là độ dài ba cạnh của một tam giác
nên a<c+b; a>c-b
=>a-c-b<0; a-c+b>0
=>(a-c-b)(a-c+b)<0
=>\(a^2+c^2< b^2+2ac\)
=>Loại B
\(b^2+c^2-a^2-2bc=\left(b-c\right)^2-a^2\)
=(b-c-a)(b-c+a)
Vì a,b,c là độ dài ba cạnh của một tam giác nên b<c+a; b>c-a
=>b-c-a<0; b-c+a>0
=>(b-c-a)(b-c+a)<0
=>\(b^2+c^2< a^2+2bc\)
=>C sai
=>Chọn C


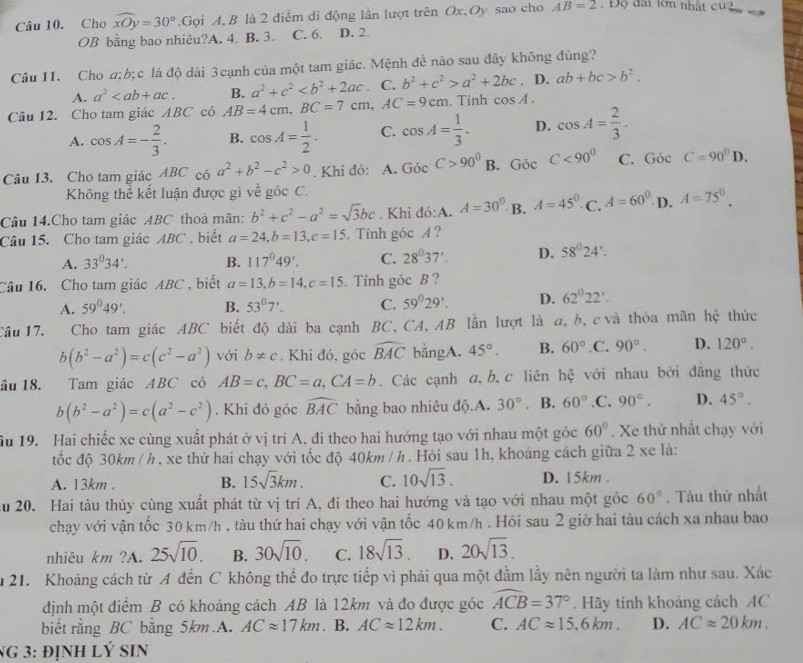




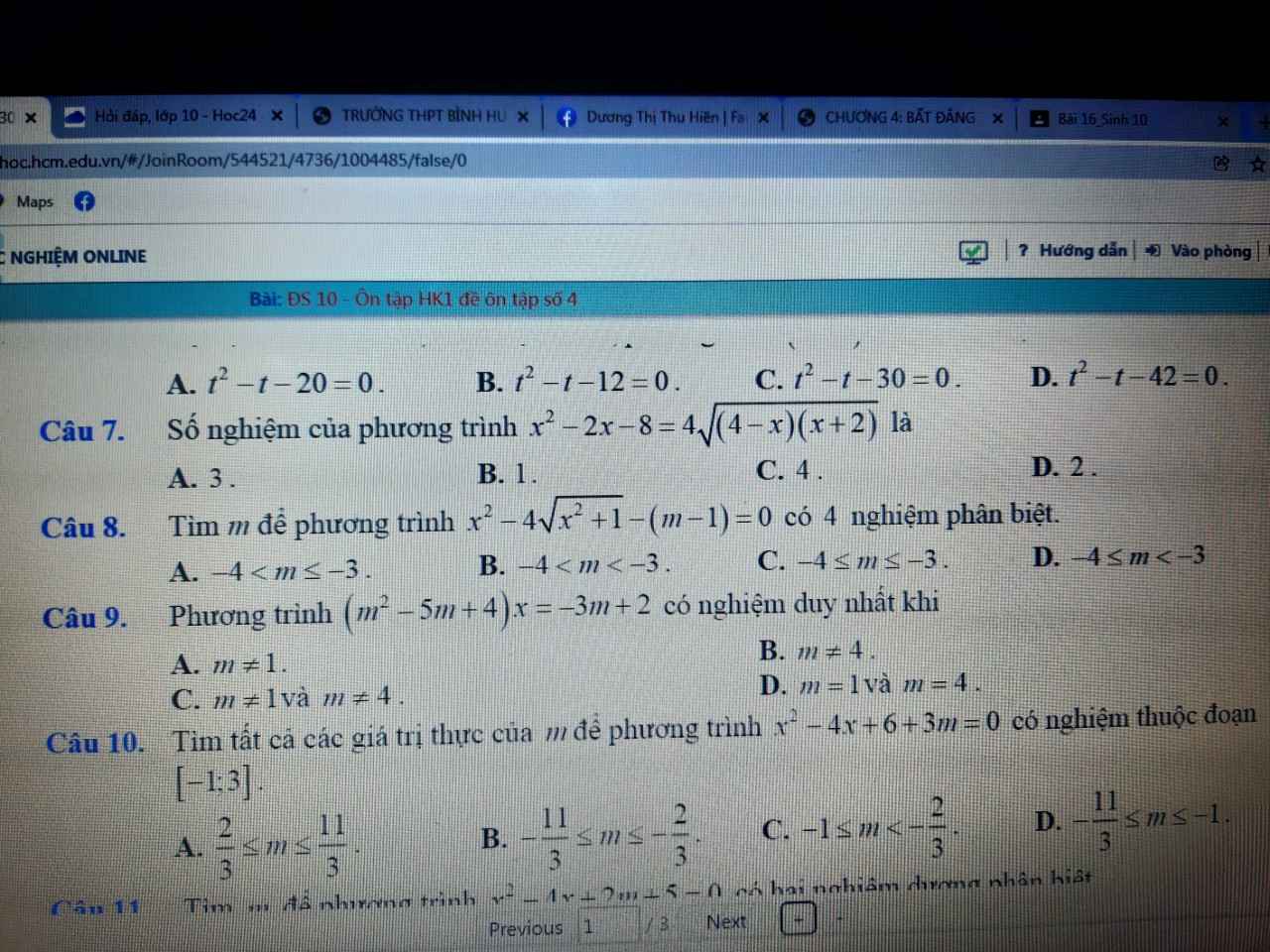
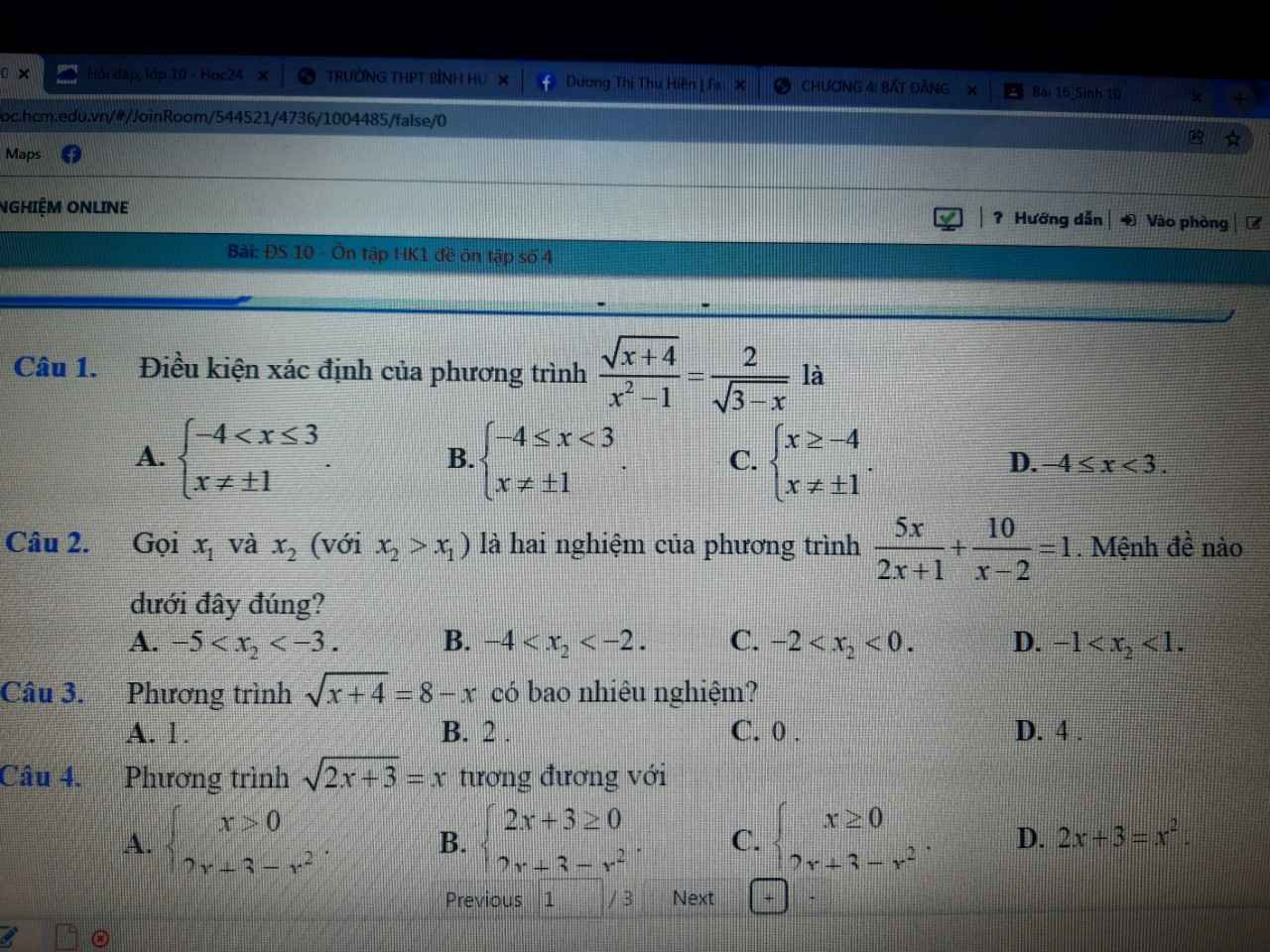
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn