a) Vì AB // CD ⇒ \(\widehat{ABD}=\widehat{ODC}\) ( 2 góc so le trong )
Hay \(\widehat{ABO}=\widehat{ODC}\)
Xét △ AOB và △ COD có:
\(\widehat{ABO}=\widehat{CDO}\) ( chứng minh trên )
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh )
⇒ △ AOB ∼ △ COD ( g - g )
b) Vì △ AOB ∼ △ COD
⇒ \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\Rightarrow\dfrac{OA}{6}=\dfrac{5}{10}\)
\(\Rightarrow OA=3cm\)
Vì OE // DC nên theo định lí Ta - lét ta có:
\(\dfrac{OE}{BC}=\dfrac{OA}{AC}\Rightarrow\dfrac{OE}{10}=\dfrac{3}{3+6}\)
\(\Rightarrow OE\approx3,3cm\)
Đúng 1
Bình luận (0)
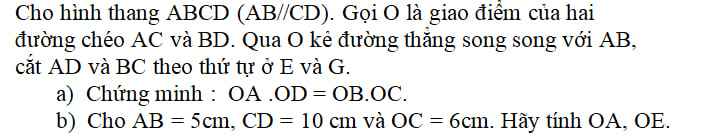
giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ
