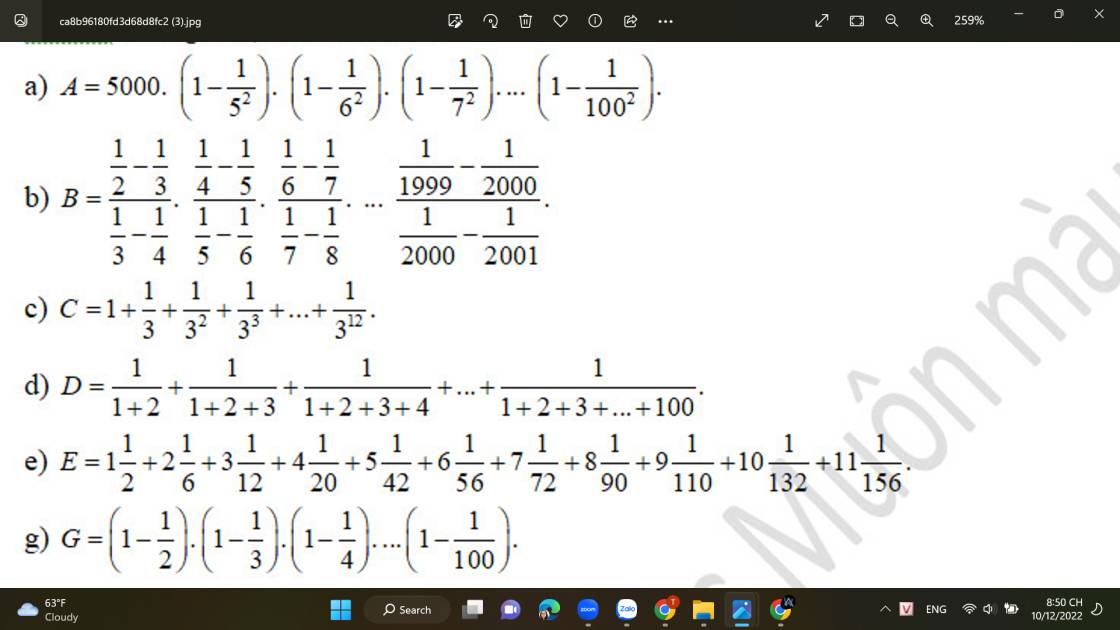
a: \(=5000\cdot\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{6}\right)\cdot...\cdot\left(1-\dfrac{1}{100}\right)\cdot\left(1+\dfrac{1}{5}\right)\cdot\left(1+\dfrac{1}{6}\right)\cdot...\cdot\left(1+\dfrac{1}{100}\right)\)
\(=5000\cdot\dfrac{4}{5}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{99}{100}\cdot\dfrac{6}{5}\cdot\dfrac{7}{6}\cdot...\cdot\dfrac{101}{100}\)
\(=5000\cdot\dfrac{4}{100}\cdot\dfrac{101}{5}=4040\)
b: Sửa đề: \(\cdot...\dfrac{\dfrac{1}{2000}-\dfrac{1}{2001}}{\dfrac{1}{2001}-\dfrac{1}{2002}}\)
\(=\dfrac{\dfrac{1}{2\cdot3}}{\dfrac{1}{3\cdot4}}\cdot\dfrac{\dfrac{1}{4\cdot5}}{\dfrac{1}{5\cdot6}}\cdot...\cdot\dfrac{\dfrac{1}{2000\cdot2001}}{\dfrac{1}{2001\cdot2002}}\)
\(=\dfrac{3\cdot4}{2\cdot3}\cdot\dfrac{5\cdot6}{4\cdot5}\cdot...\cdot\dfrac{2001\cdot2002}{2000\cdot2001}\)
\(=\dfrac{4}{2}\cdot\dfrac{6}{4}\cdot...\cdot\dfrac{2002}{2000}=\dfrac{2002}{2}=1001\)