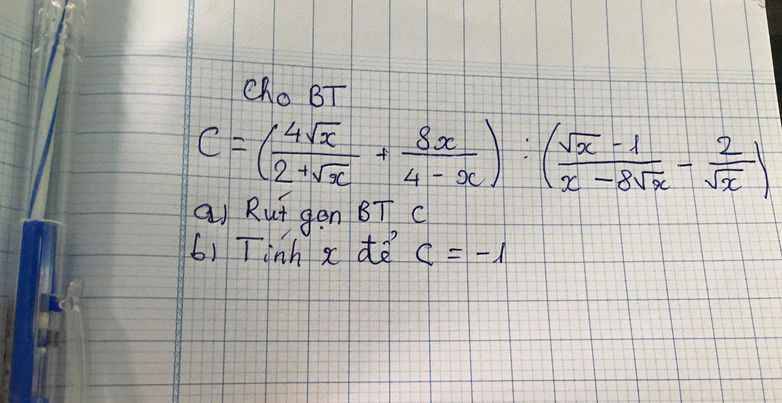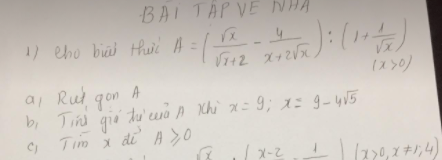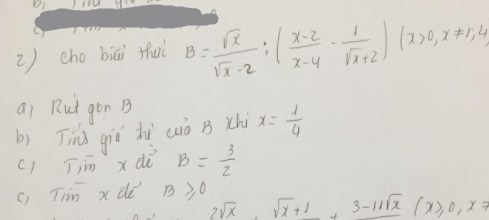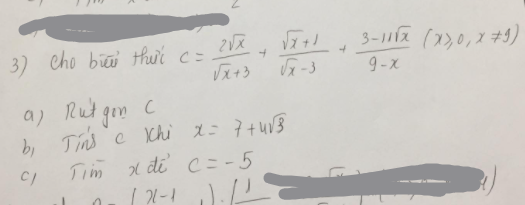\(a,M=\dfrac{3-1}{3}=\dfrac{2}{3}\\ b,P=\dfrac{x-3\sqrt{x}+2+2+8\sqrt{x}+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}+6\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ c,Q=\dfrac{\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}+\dfrac{x-5}{\sqrt{x}}=\dfrac{\sqrt{x}+6+x-5}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\\ Q=\sqrt{x}+1+\dfrac{1}{\sqrt{x}}\ge2\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}+1=2+1=3\)
Vậy \(Q\ge3\)