1) \(M=\left(2x-1\right)\left(2y-1\right)\)
\(\Rightarrow M=4xy-2x-2y+1\)
\(\Rightarrow M=4xy-2\left(x+y\right)+1\)
-Thay \(x+y=10\) và \(xy=16\) vào M, ta được:
\(M=4.16-2.10+1=45\)
2) \(N=2x-2y+13x^2y^2\left(x-y\right)+15\left(y^2x-x^2y\right)+\left|\dfrac{2015}{2016}\right|^0\)
\(\Rightarrow N=2\left(x-y\right)+13x^2y^2\left(x-y\right)+15xy\left(y-x\right)+1\)
\(\Rightarrow N=2\left(x-y\right)+13x^2y^2\left(x-y\right)-15xy\left(x-y\right)+1\)
-Thay \(x-y=0\) vào N ta được:
\(N=2.0+13x^2y^2.0-15xy.0+1=1\)
3) -Ta có: \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
\(\Rightarrow\dfrac{yz+xz+xy}{xyz}=0\)
-Vì \(xyz\ne0\) nên \(yz+xz+xy=0\)
\(\Rightarrow\left[{}\begin{matrix}yz=-xz-xy=-x\left(y+z\right)\\xz=-yz-xy=-y\left(x+z\right)\\xy=-yz-xz=-z\left(x+y\right)\end{matrix}\right.\)
-Thay \(\left[{}\begin{matrix}yz=-x\left(y+z\right)\\xz=-y\left(x+z\right)\\xy=-z\left(x+y\right)\end{matrix}\right.\) vào P ta được:
\(P=\left(-\dfrac{z\left(x+y\right)}{z^2}-\dfrac{x\left(y+z\right)}{x^2}-\dfrac{y\left(x+z\right)}{y^2}-2\right)^{2013}\)
\(\Rightarrow P=\left(-\dfrac{x+y}{z}-\dfrac{y+z}{x}-\dfrac{x+z}{y}-2\right)^{2013}\)
\(\Rightarrow P=\left(-\dfrac{xy\left(x+y\right)+yz\left(y+z\right)+zx\left(x+z\right)-2xyz}{xyz}\right)^{2013}\)
\(\Rightarrow P=\left(-\dfrac{-xyz-xyz-xyz-2xyz}{xyz}\right)^{2013}\)
\(\Rightarrow P=\left(\dfrac{5xyz}{xyz}\right)^{2013}=5^{2013}\).
4) -Ta có: \(\left(x-2\right)^4\ge0;\left(2y-1\right)^{2014}\ge0\)
\(\Rightarrow\left(x-2\right)^4+\left(2y-1\right)^{2014}\ge0\)
Mà \(\left(x-2\right)^4+\left(2y-1\right)^{2014}\le0\) (đề bài cho).
\(\Rightarrow\left(x-2\right)^4+\left(2y-1\right)^{2014}=0\)
\(\Rightarrow\left(x-2\right)^4=0\) và \(\left(2y-1\right)^{2014}=0\)
\(\Rightarrow x=2\) và \(y=\dfrac{1}{2}\).
-Thay \(x=2\) và \(y=\dfrac{1}{2}\) vào Q, ta được:
\(Q=21.2^2.\dfrac{1}{4} +4.2.\left(\dfrac{1}{4}\right)^2=\dfrac{43}{2}\)






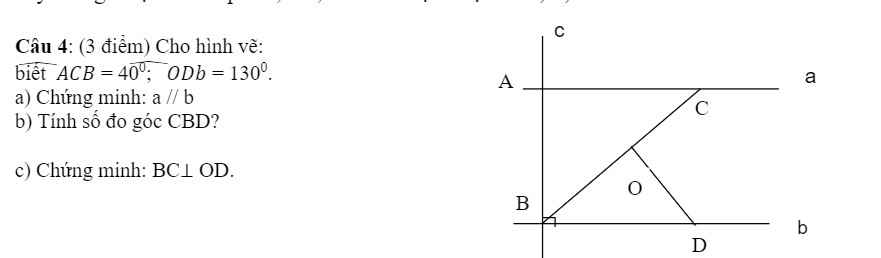 mk vs ạ
mk vs ạ





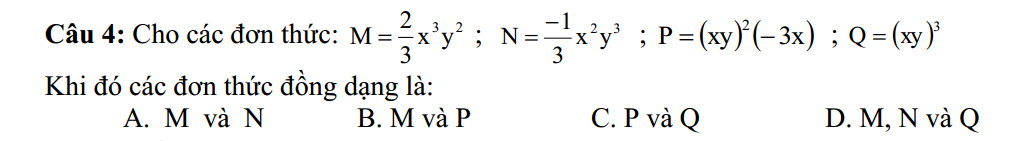 giúp mk vs, mk cần gấp
giúp mk vs, mk cần gấp





