a, Theo hình vẽ
\(m\perp p\)
\(n\perp p\)
\(\Rightarrow m//n\) ( từ vuông góc đến song song )
b, Ta có \(m//n\left(cmt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_4}=50^o\) ( hai góc so le trong )
\(\widehat{B_4}=\widehat{B_2}=50^o\) ( hai góc đối đỉnh)
Lại có \(\widehat{B_1}+\widehat{B_2}=180^o\) ( hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-50^o=130^o\)
\(\widehat{B_1}=\widehat{B_3}=130^o\) ( hai góc đối đỉnh)
\(@Thv\)
a,Ta có:
\(\widehat{A1}=\widehat{B4}=50^o\)
Mà 2 góc này ở vị trí sole trong nên m//n(dhnb)
b,Ta có:\(\widehat{B4}=50^O\left(cmt\right)\)
\(\widehat{B1}+\widehat{B4}=180^o\left(kềbù\right)\)
\(\Rightarrow\widehat{B1}=180^0-\widehat{B4}\\ \Rightarrow\widehat{B1}=180^0-50^0=130^0\)
\(\widehat{B2}=\widehat{B4}=50^0\left(dốiđỉnh\right)\)
\(\widehat{B3}=\widehat{B1}=130^0\left(dốiđỉnh\right)\)
Vậy \(\widehat{B3}=\widehat{B1}=130^0;\widehat{B4}=\widehat{B2}=50^0\)
Giải:
a) Vì m ⊥ P
n ⊥ P
⇒ m // n (từ vuông góc -> song song)
b) Vì m // n (cm câu a) ⇒ Góc A1 = Góc B2 (2 góc so le trong)
⇒ Góc A1 = Góc B2 = 500
Vì góc B1 và B2 là 2 góc kề bù ⇒ Góc B1 + Góc B2 = 1800
⇒ Góc B1 = 1300
Vì góc B2 và B3 là 2 góc kề bù ⇒ Góc B2 + Góc B3 = 1800
⇒ Góc B3 = 1300
Vì góc B3 và B4 là 2 góc kề bù ⇒ Góc B3 + B4 = 1800
⇒ Góc B4 = 500
Vậy Góc B1 = 1300; B2 = 1300; B3 = 1300; B4 = 500
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
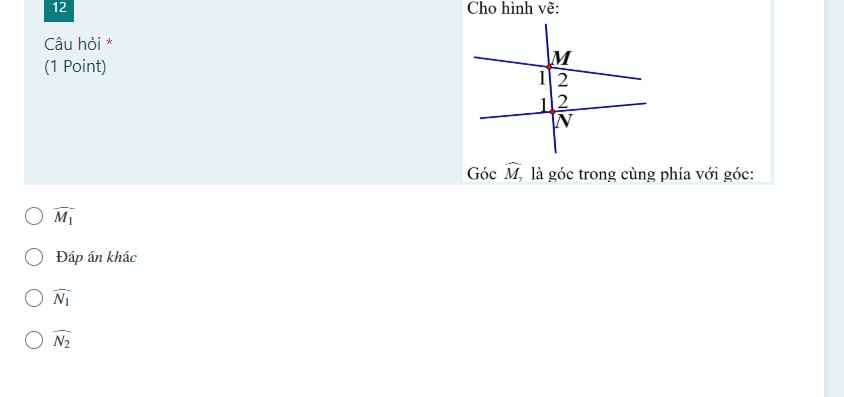cảm ơn!
.
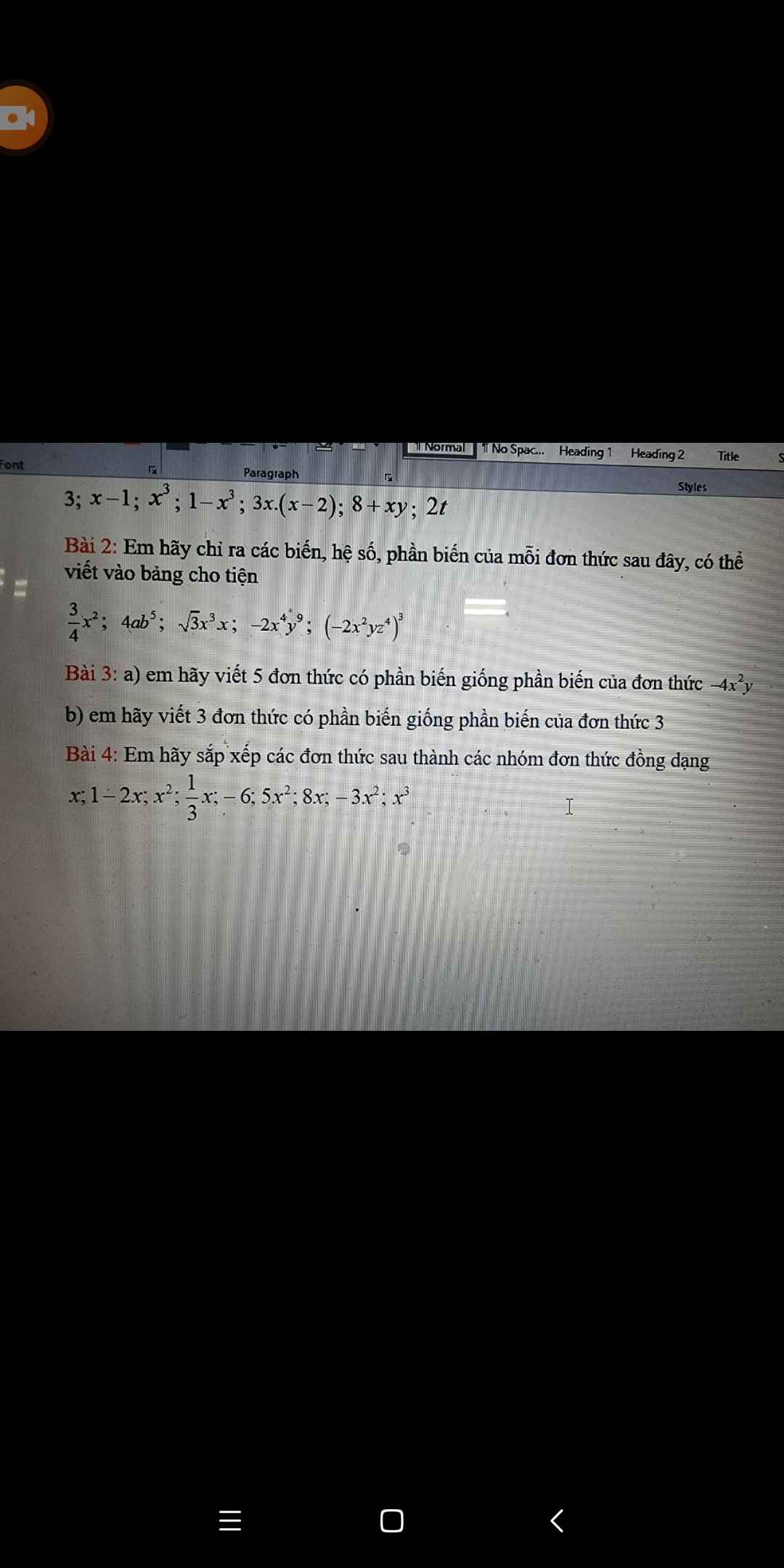