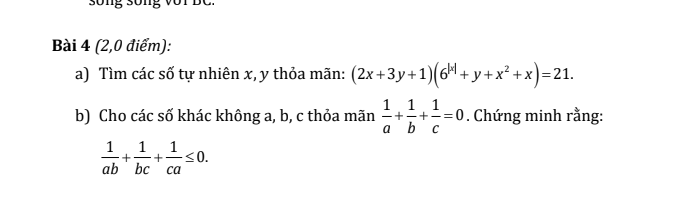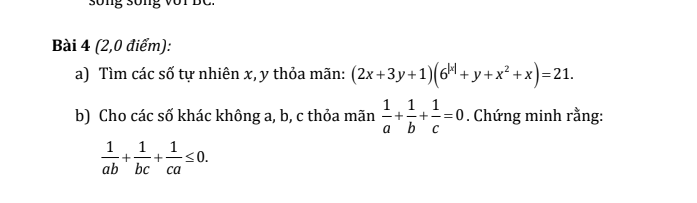Question

Giúp mk với mn ơiiii

Answer 1

\(b,\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\\ \Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2=0\\ \Rightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)=0\\ \Rightarrow2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)=-\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)

Vì \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge0\Rightarrow2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\le0\)

Vậy \(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\le0\)