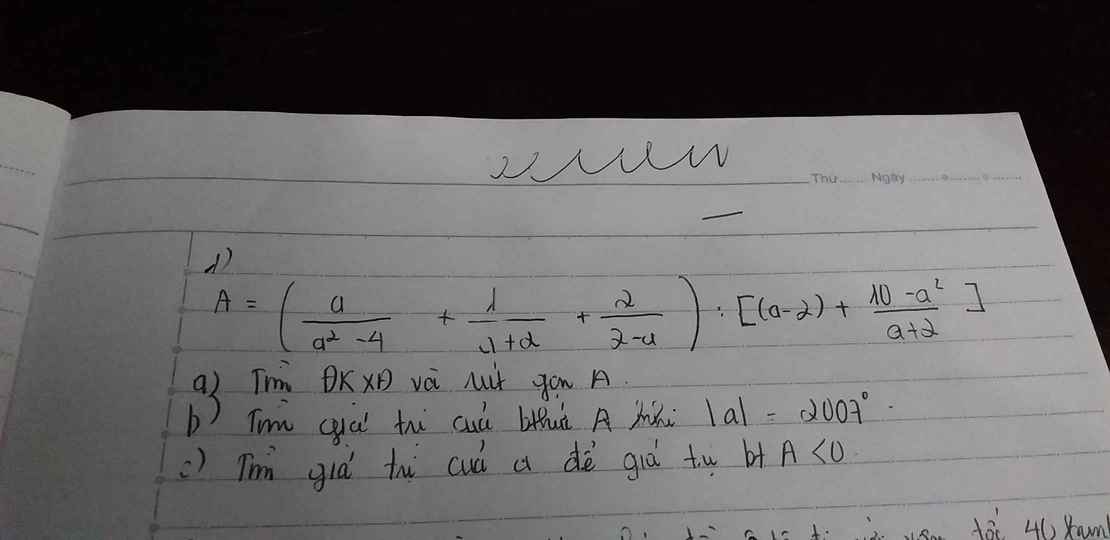a) ĐKXĐ \(\left\{{}\begin{matrix}a^2-4\ne0\\a+2\ne0\\2-a\ne0\\a-2+\dfrac{10-a^2}{a+2}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne2\\a\ne-2\\\dfrac{a^2-4+10-a^2}{a+2}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne2\\a\ne-2\end{matrix}\right.\)
Ta có:
\( A=\left(\dfrac{a}{a^2-4}+\dfrac{1}{a+2}+\dfrac{2}{2-a}\right):\left[\left(a-2\right)+\dfrac{10-a^2}{a+2}\right]\\ =\dfrac{a+\left(a-2\right)-2\left(a+2\right)}{\left(a-2\right)\left(a+2\right)}:\dfrac{a^2-4+10-a^2}{a+2}\\ =\dfrac{-6}{\left(a-2\right)\left(a+2\right)}\cdot\dfrac{a+2}{6}=\dfrac{-1}{a-2}\)
b) Để
\(A=-\dfrac{1}{a-2}=2007^0=1\\ \Rightarrow a-2=-1\Leftrightarrow a=1\left(t.m\right)\)
c) Để A<0
\(\Leftrightarrow\dfrac{-1}{a-2}< 0\Leftrightarrow a-2>0\Leftrightarrow a>2\left(t.m\right)\)