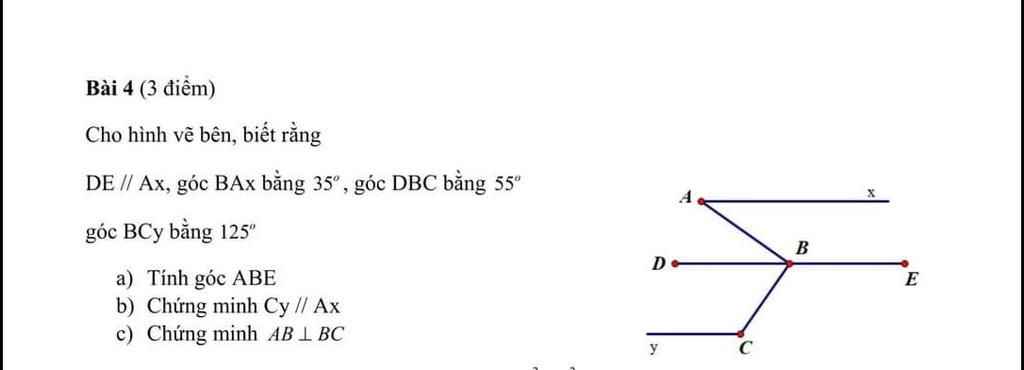a, \(S=\dfrac{3\cdot\left(\dfrac{1}{13}-0,2+\dfrac{1}{7}+0.25\right)}{11\cdot\left(\dfrac{1}{7}-0.2+\dfrac{1}{13}+0.25\right)}=\dfrac{3}{11}\)
b, Ta có: \(\dfrac{1}{3}A=-\dfrac{1}{3^2}+\dfrac{1}{3^3}-\dfrac{1}{3^4}+...+\dfrac{1}{3^{101}}\)
\(\Rightarrow A+\dfrac{1}{3}A=-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^2}-\dfrac{1}{3^3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}-\dfrac{1}{3^{100}}+\dfrac{1}{3^{101}}\)
\(\Rightarrow\dfrac{4}{3}A=-\dfrac{1}{3}+\dfrac{1}{3^{101}}\)
hay \(A=-\dfrac{1}{4}+\dfrac{1}{4}\cdot\dfrac{1}{3^{100}}=\dfrac{1}{4}\cdot\left(\dfrac{1}{3^{100}}-1\right)\)
\(\Rightarrow B=4\left|A\right|+\dfrac{1}{3^{100}}=\left|4A\right|+\dfrac{1}{3^{100}}=\left|\dfrac{1}{3^{100}}-1\right|+\dfrac{1}{3^{100}}=1-\dfrac{1}{3^{100}}+\dfrac{1}{3^{100}}=1\)
Có chỗ nào chưa hiểu thì bạn cứ hỏi nha.
Chúc bạn học tốt!

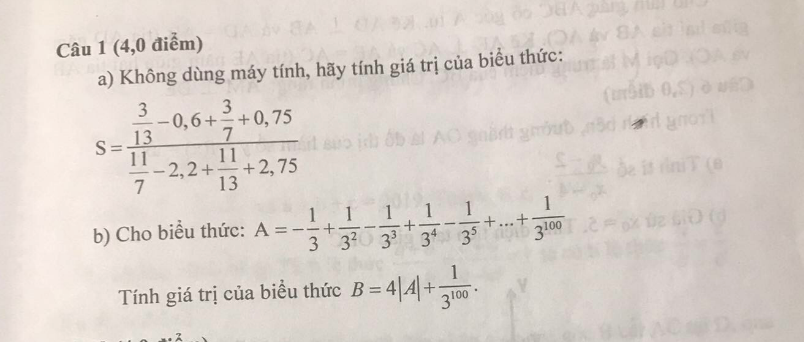









 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!! giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha