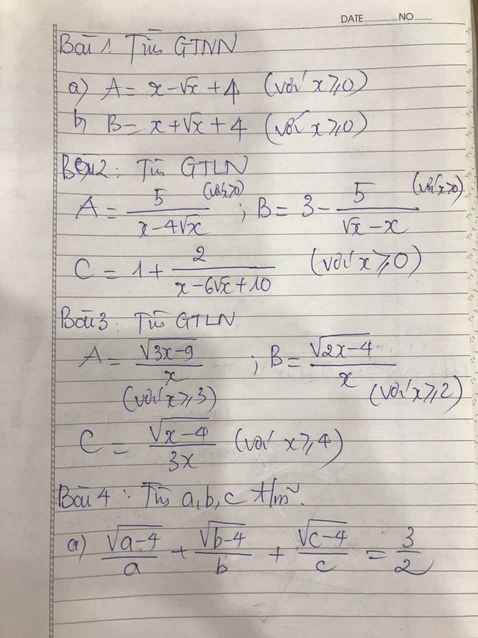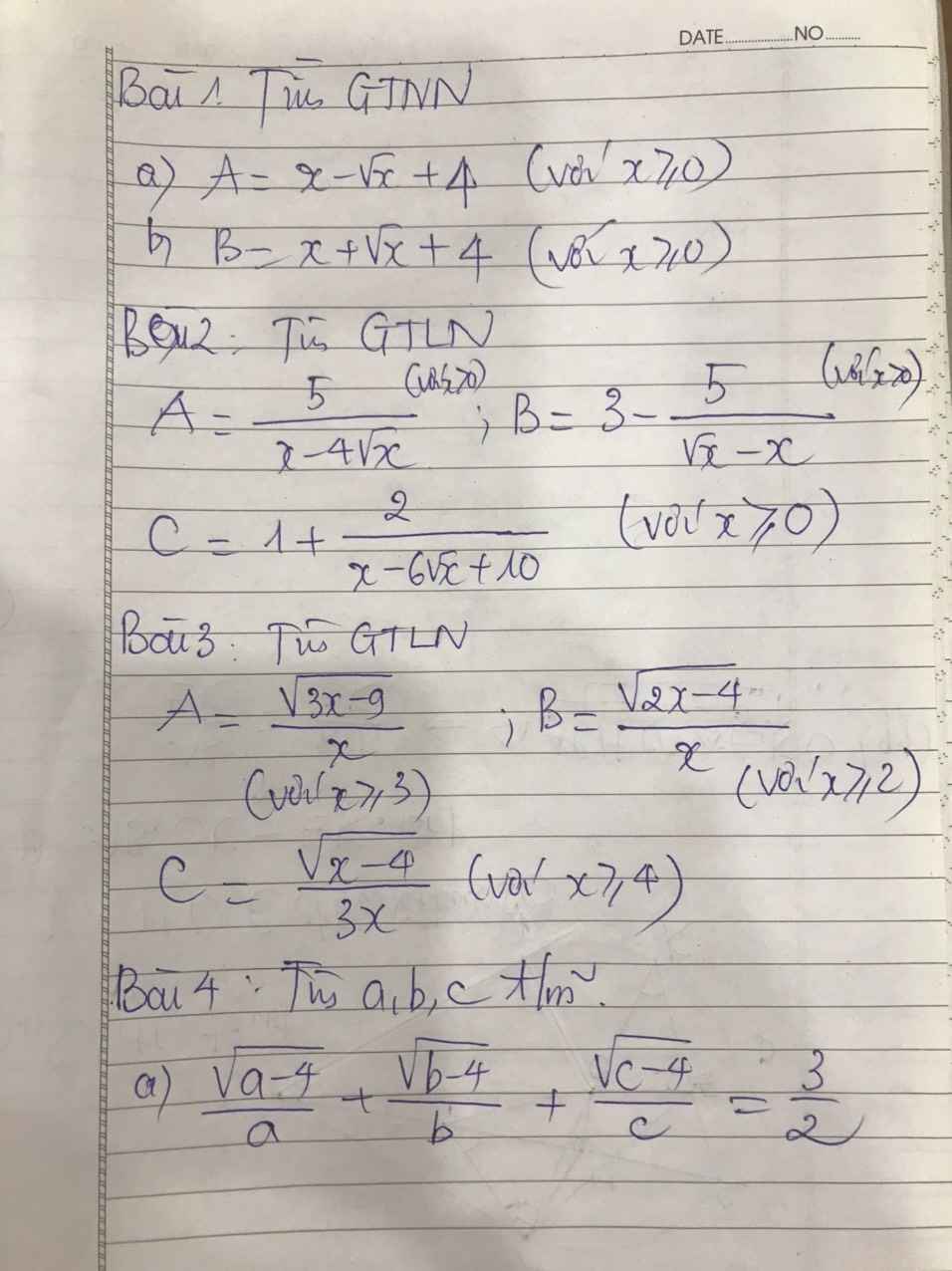B1)
b, Có \(x\ge0\Rightarrow B=x+\sqrt{x}+4\ge0+0+4=4\)
Dấu "=" xảy ra khi x=0
Vậy \(B_{min}=4\)
Bài 1 :
\(b,B=x+\sqrt{x}+4=x+2.\sqrt{x}.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{15}{4}\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\)
Thấy : \(\sqrt{x}+\dfrac{1}{2}\ge\dfrac{1}{2}\)
\(\Rightarrow B=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ge4\)
Vậy \(Min_B=4\Leftrightarrow x=0\)
Bài 1 :
b)
\(B=x+\sqrt{x}+4=\left(\sqrt{x}\right)^2+2.\dfrac{1}{2}\sqrt{x}+\dfrac{1}{4}-\dfrac{1}{4}+4=\left(\sqrt{x}+\dfrac{1}{2}\right)+\dfrac{15}{14}\)
\(\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+\dfrac{1}{2}\ge\dfrac{1}{2}\)
Vậy Max B = \(\left(\dfrac{1}{2}\right)^2+\dfrac{15}{4}=4\)
Dấu = xảy ra khi \(\sqrt{x}=0\Leftrightarrow x=0\)